Применение кластерного анализа в Microsoft Excel

Одним из инструментов для решения экономических задач является кластерный анализ. С его помощью кластеры и другие объекты массива данных классифицируются по группам. Данную методику можно применять в программе Excel. Посмотрим, как это делается на практике.

Использование кластерного анализа

С помощью кластерного анализа можно проводить выборку по признаку, который исследуется. Его основная задача – разбиение многомерного массива на однородные группы. В качестве критерия группировки применяется парный коэффициент корреляции или эвклидово расстояние между объектами по заданному параметру. Наиболее близкие друг к другу значения группируются вместе.

Хотя чаще всего данный вид анализа применяют в экономике, его также можно использовать в биологии (для классификации животных), психологии, медицине и во многих других сферах деятельности человека. Кластерный анализ можно применять, используя для этих целей стандартный набор инструментов Эксель.

Пример использования

Имеем пять объектов, которые характеризуются по двум изучаемым параметрам – x и y.

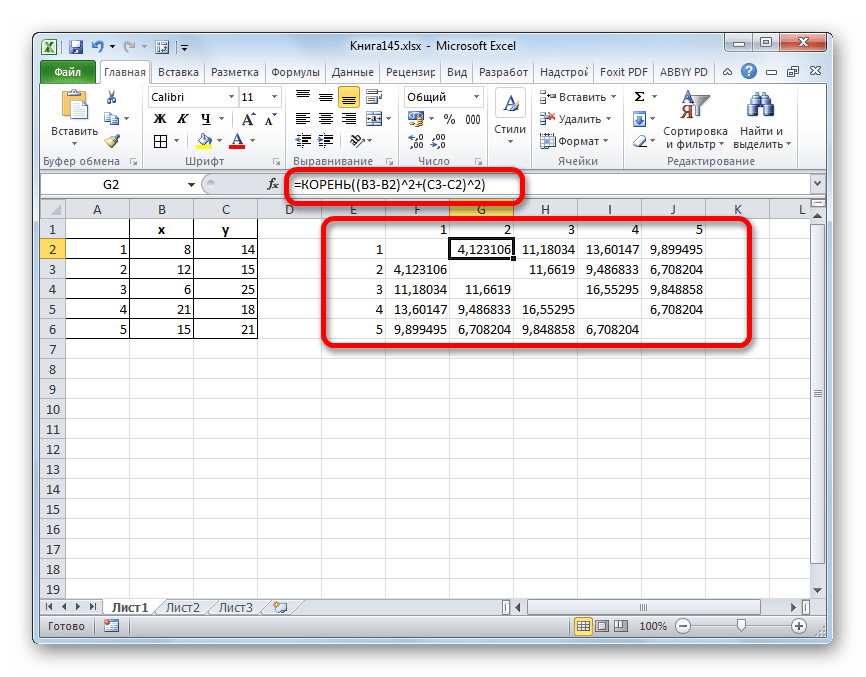
1. Применяем к данным значениям формулу эвклидового расстояния, которое вычисляется по шаблону:

   =КОРЕНЬ((x2-x1)^2+(y2-y1)^2)


2. Данное значение вычисляем между каждым из пяти объектов. Результаты расчета помещаем в матрице расстояний.

3. Смотрим, между какими значениями дистанция меньше всего. В нашем примере — это объекты 1 и 2. Расстояние между ними составляет 4,123106, что меньше, чем между любыми другими элементами данной совокупности.

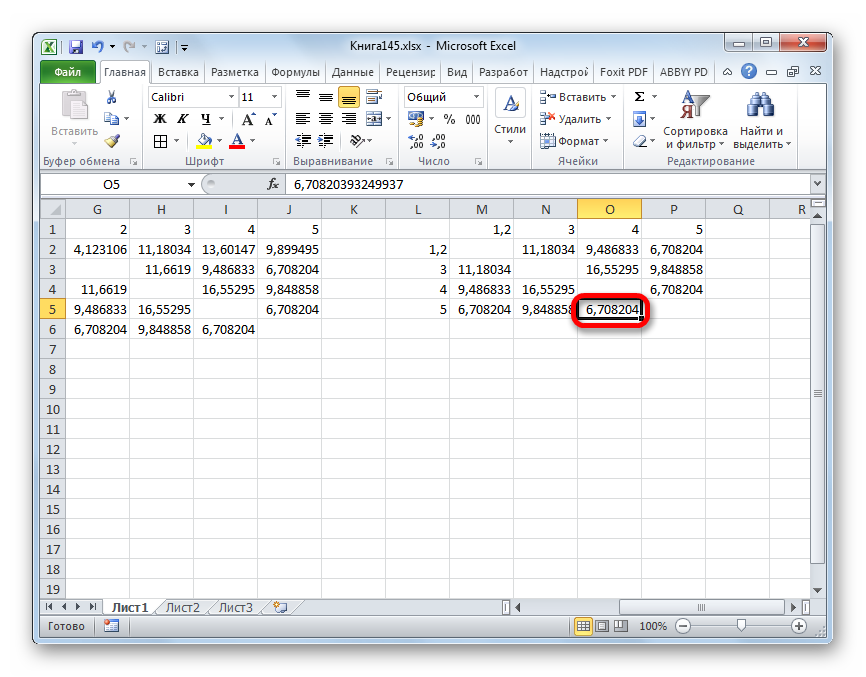
4. Объединяем эти данные в группу и формируем новую матрицу, в которой значения 1,2 выступают отдельным элементом. При составлении матрицы оставляем наименьшие значения из предыдущей таблицы для объединенного элемента. Опять смотрим, между какими элементами расстояние минимально. На этот раз – это 4 и 5, а также объект 5 и группа объектов 1,2. Дистанция составляет 6,708204.

5. Добавляем указанные элементы в общий кластер. Формируем новую матрицу по тому же принципу, что и в предыдущий раз. То есть, ищем самые меньшие значения. Таким образом мы видим, что нашу совокупность данных можно разбить на два кластера. В первом кластере находятся наиболее близкие между собой элементы – 1,2,4,5. Во втором кластере в нашем случае представлен только один элемент — 3. Он находится сравнительно в отдалении от других объектов. Расстояние между кластерами составляет 9,84.

На этом завершается процедура разбиения совокупности на группы.

Как видим, хотя в целом кластерный анализ и может показаться сложной процедурой, но на самом деле разобраться в нюансах данного метода не так уж тяжело. Главное понять основную закономерность объединения в группы.

Наш Telegram каналТолько полезная информация