Все способы:
Одним из показателей, описывающих качество построенной модели в статистике, является коэффициент детерминации (R^2), который ещё называют величиной достоверности аппроксимации. С его помощью можно определить уровень точности прогноза. Давайте узнаем, как можно произвести расчет данного показателя с помощью различных инструментов программы Excel.
Вычисление коэффициента детерминации
В зависимости от уровня коэффициента детерминации, принято разделять модели на три группы:
| 0,8 – 1 | Модель хорошего качества |
| 0,5 – 0,8 | Модель приемлемого качества |
| 0 – 0,5 | Модель плохого качества |
В последнем случае качество модели говорит о невозможности её использования для прогноза.
Выбор способа вычисления указанного значения в Excel зависит от того, является ли регрессия линейной или нет. В первом случае можно использовать функцию КВПИРСОН, а во втором придется воспользоваться специальным инструментом из пакета анализа.
Способ 1: вычисление коэффициента детерминации при линейной функции
Прежде всего, выясним, как найти коэффициент детерминации при линейной функции. В этом случае данный показатель будет равняться квадрату коэффициента корреляции. Произведем его расчет с помощью встроенной функции Excel на примере конкретной таблицы, которая приведена ниже.
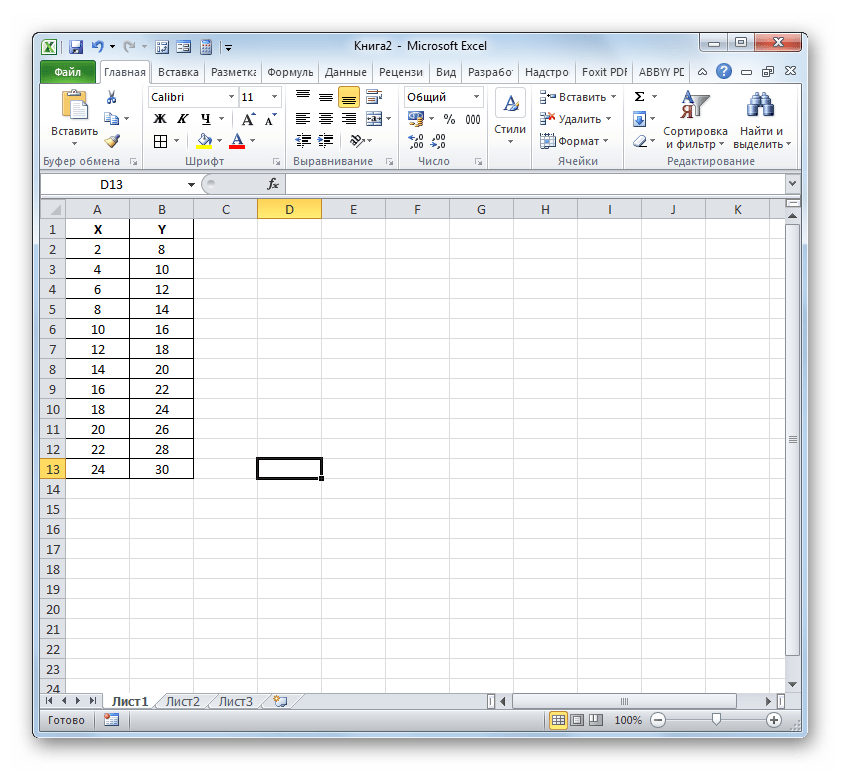
- Выделяем ячейку, где будет произведен вывод коэффициента детерминации после его расчета, и щелкаем по пиктограмме «Вставить функцию».
- Запускается Мастер функций. Перемещаемся в его категорию «Статистические» и отмечаем наименование «КВПИРСОН». Далее клацаем по кнопке «OK».
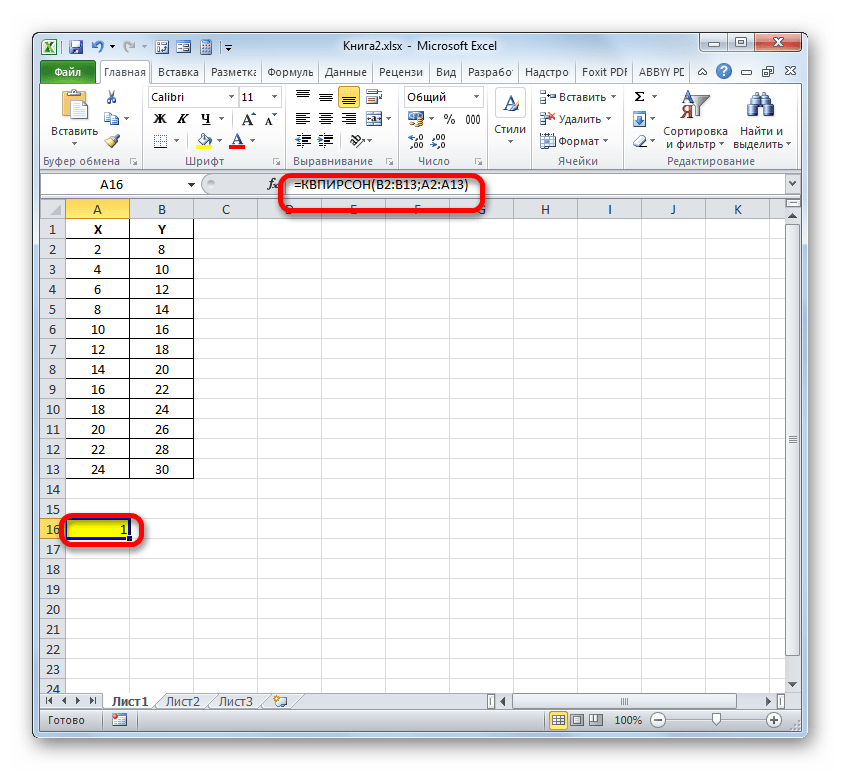
- Происходит запуск окна аргументов функции КВПИРСОН. Данный оператор из статистической группы предназначен для вычисления квадрата коэффициента корреляции функции Пирсона, то есть, линейной функции. А как мы помним, при линейной функции коэффициент детерминации как раз равен квадрату коэффициента корреляции.
Синтаксис этого оператора такой:
=КВПИРСОН(известные_значения_y;известные_значения_x)Таким образом, функция имеет два оператора, один из которых представляет собой перечень значений функции, а второй – аргументов. Операторы могут быть представлены, как непосредственно в виде значений, перечисленных через точку с запятой (;), так и в виде ссылок на диапазоны, где они расположены. Именно последний вариант и будет использован нами в данном примере.
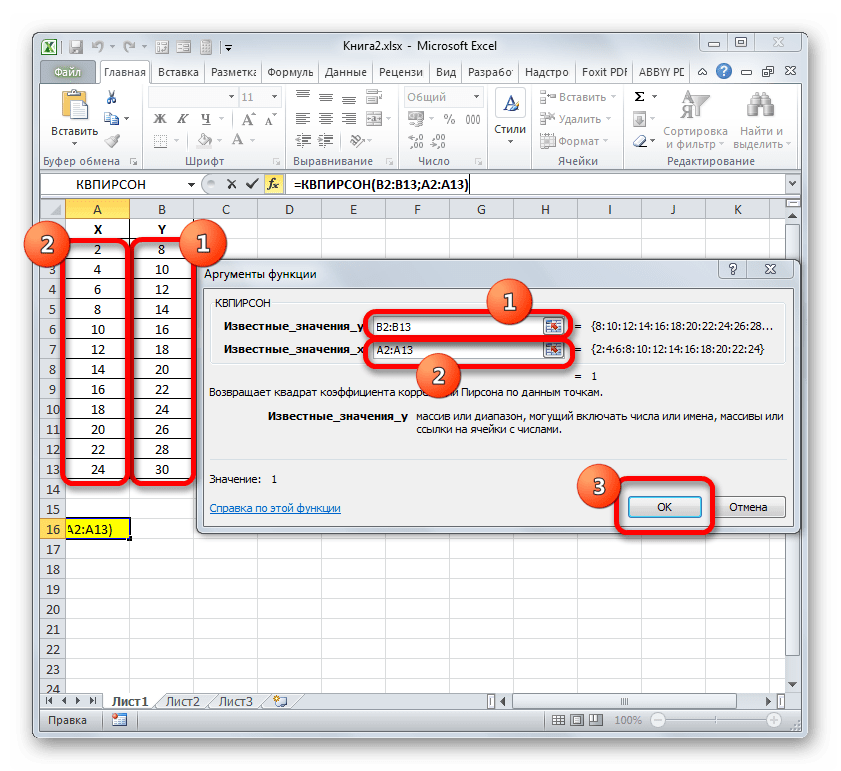
Устанавливаем курсор в поле «Известные значения y». Выполняем зажим левой кнопки мышки и производим выделение содержимого столбца «Y» таблицы. Как видим, адрес указанного массива данных тут же отображается в окне.
Аналогичным образом заполняем поле «Известные значения x». Ставим курсор в данное поле, но на этот раз выделяем значения столбца «X».
После того, как все данные были отображены в окне аргументов КВПИРСОН, клацаем по кнопке «OK», расположенной в самом его низу.
- Как видим, вслед за этим программа производит расчет коэффициента детерминации и выдает результат в ту ячейку, которая была выделена ещё перед вызовом Мастера функций. В нашем примере значение вычисляемого показателя получилось равным 1. Это значит, что представленная модель абсолютно достоверная, то есть, исключает погрешность.
Урок: Мастер функций в Microsoft Excel
Способ 2: вычисление коэффициента детерминации в нелинейных функциях
Но указанный выше вариант расчета искомого значения можно применять только к линейным функциям. Что же делать, чтобы произвести его расчет в нелинейной функции? В Экселе имеется и такая возможность. Её можно осуществить с помощью инструмента «Регрессия», который является составной частью пакета «Анализ данных».
- Но прежде, чем воспользоваться указанным инструментом, следует активировать сам «Пакет анализа», который по умолчанию в Экселе отключен. Перемещаемся во вкладку «Файл», а затем переходим по пункту «Параметры».
- В открывшемся окне производим перемещение в раздел «Надстройки» при помощи навигации по левому вертикальному меню. В нижней части правой области окна располагается поле «Управление». Из списка доступных там подразделов выбираем наименование «Надстройки Excel…», а затем щелкаем по кнопке «Перейти…», расположенной справа от поля.
- Производится запуск окна надстроек. В центральной его части расположен список доступных надстроек. Устанавливаем флажок около позиции «Пакет анализа». Вслед за этим требуется щелкнуть по кнопке «OK» в правой части интерфейса окна.
- Пакет инструментов «Анализ данных» в текущем экземпляре Excel будет активирован. Доступ к нему располагается на ленте во вкладке «Данные». Перемещаемся в указанную вкладку и клацаем по кнопке «Анализ данных» в группе настроек «Анализ».
- Активируется окошко «Анализ данных» со списком профильных инструментов обработки информации. Выделяем из этого перечня пункт «Регрессия» и клацаем по кнопке «OK».
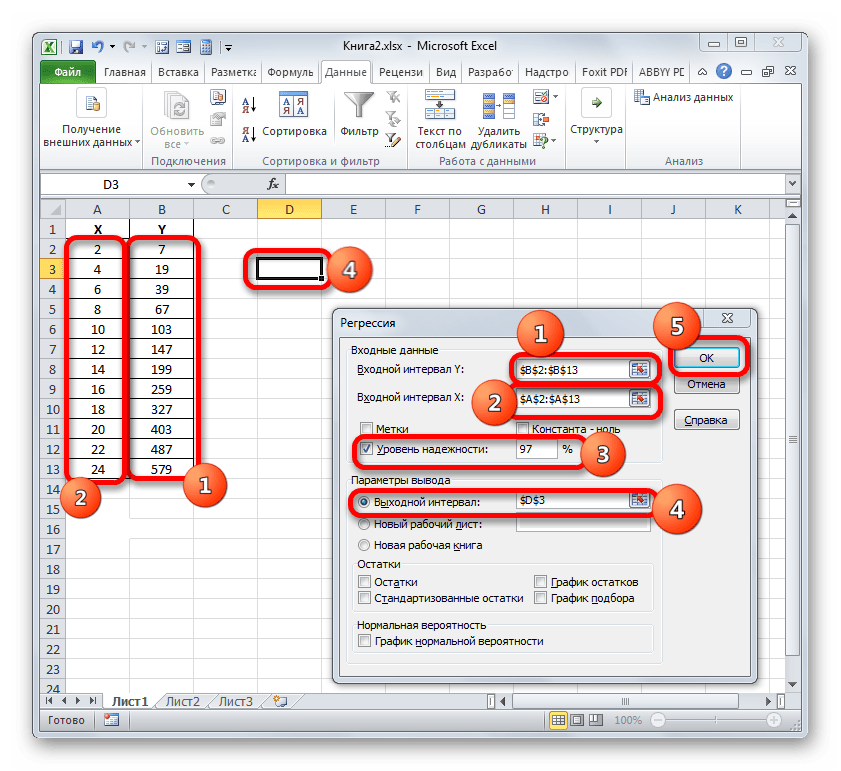
- Затем открывается окно инструмента «Регрессия». Первый блок настроек – «Входные данные». Тут в двух полях нужно указать адреса диапазонов, где находятся значения аргумента и функции. Ставим курсор в поле «Входной интервал Y» и выделяем на листе содержимое колонки «Y». После того, как адрес массива отобразился в окне «Регрессия», ставим курсор в поле «Входной интервал Y» и точно таким же образом выделяем ячейки столбца «X».
Около параметров «Метка» и «Константа-ноль» флажки не ставим. Флажок можно установить около параметра «Уровень надежности» и в поле напротив указать желаемую величину соответствующего показателя (по умолчанию 95%).
В группе «Параметры вывода» нужно указать, в какой области будет отображаться результат вычисления. Существует три варианта:
- Область на текущем листе;
- Другой лист;
- Другая книга (новый файл).
Остановим свой выбор на первом варианте, чтобы исходные данные и результат размещались на одном рабочем листе. Ставим переключатель около параметра «Выходной интервал». В поле напротив данного пункта ставим курсор. Щелкаем левой кнопкой мыши по пустому элементу на листе, который призван стать левой верхней ячейкой таблицы вывода итогов расчета. Адрес данного элемента должен высветиться в поле окна «Регрессия».
Группы параметров «Остатки» и «Нормальная вероятность» игнорируем, так как для решения поставленной задачи они не важны. После этого клацаем по кнопке «OK», которая размещена в правом верхнем углу окна «Регрессия».
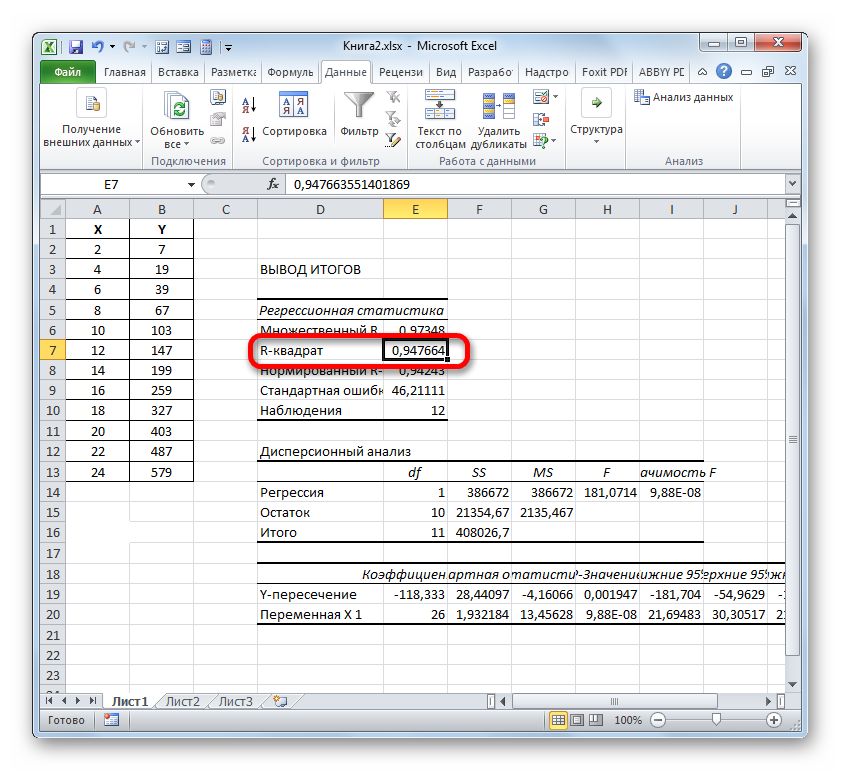
- Программа производит расчет на основе ранее введенных данных и выводит результат в указанный диапазон. Как видим, данный инструмент выводит на лист довольно большое количество результатов по различным параметрам. Но в контексте текущего урока нас интересует показатель «R-квадрат». В данном случае он равен 0,947664, что характеризует выбранную модель, как модель хорошего качества.
Способ 3: коэффициент детерминации для линии тренда
Кроме указанных выше вариантов, коэффициент детерминации можно отобразить непосредственно для линии тренда в графике, построенном на листе Excel. Выясним, как это можно сделать на конкретном примере.
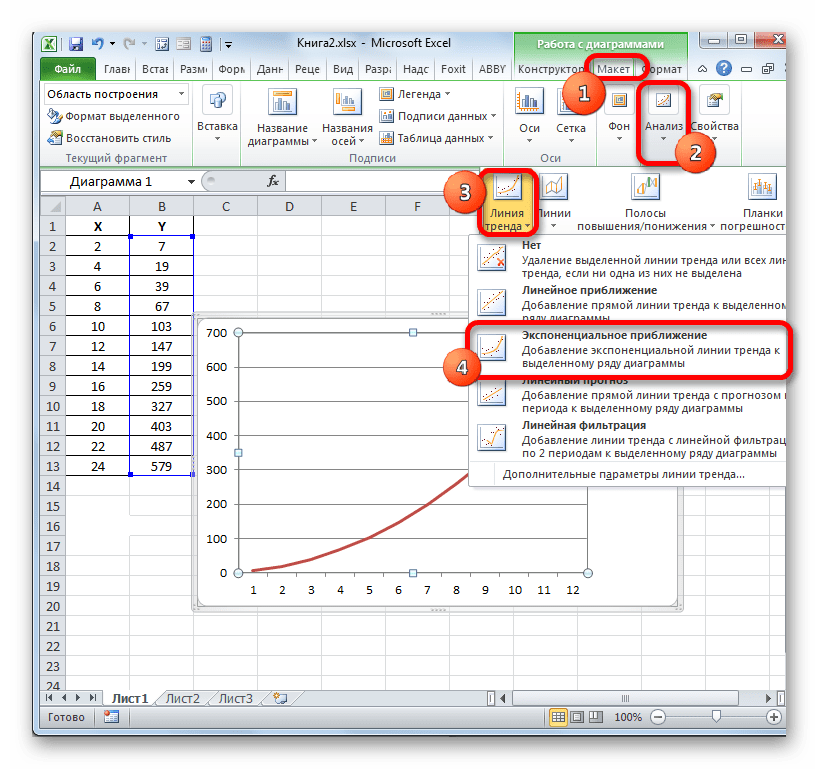
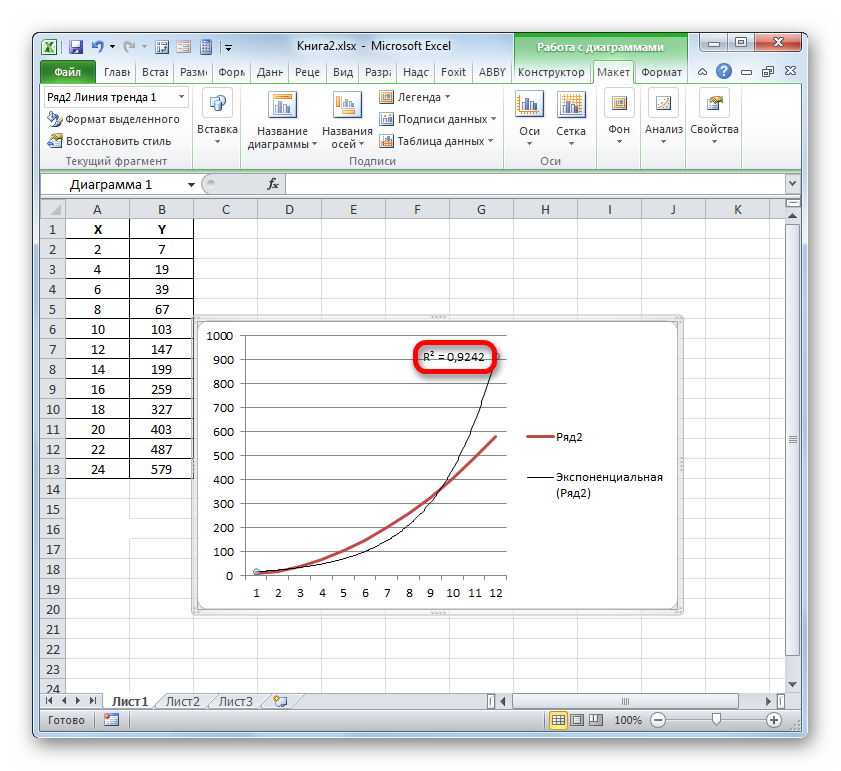
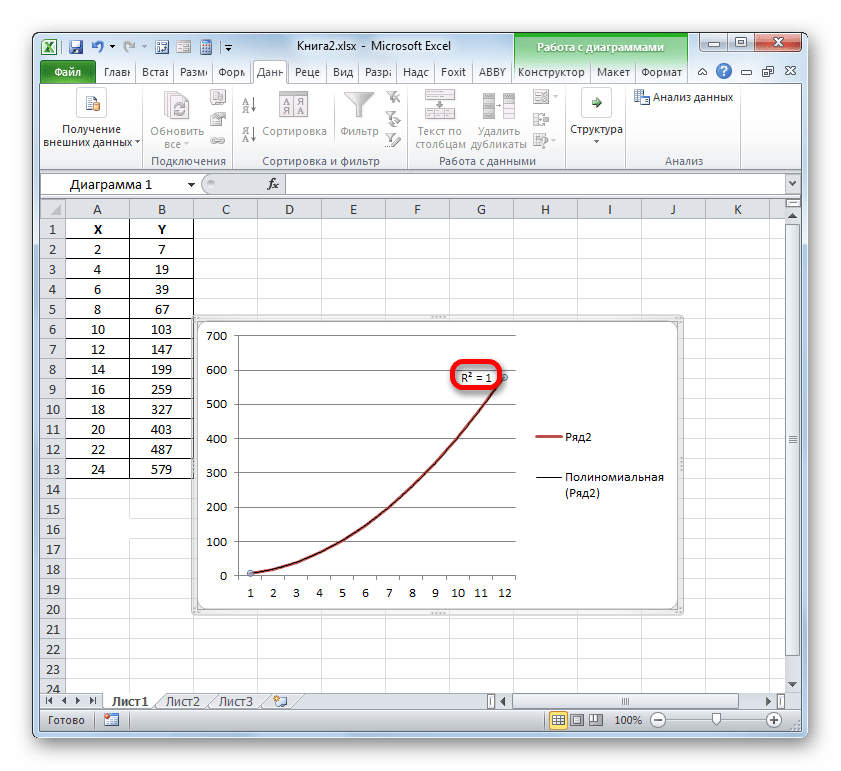
- Мы имеем график, построенный на основе таблицы аргументов и значений функции, которая была использована для предыдущего примера. Произведем построение к нему линии тренда. Кликаем по любому месту области построения, на которой размещен график, левой кнопкой мыши. При этом на ленте появляется дополнительный набор вкладок – «Работа с диаграммами». Переходим во вкладку «Макет». Клацаем по кнопке «Линия тренда», которая размещена в блоке инструментов «Анализ». Появляется меню с выбором типа линии тренда. Останавливаем выбор на том типе, который соответствует конкретной задаче. Давайте для нашего примера выберем вариант «Экспоненциальное приближение».
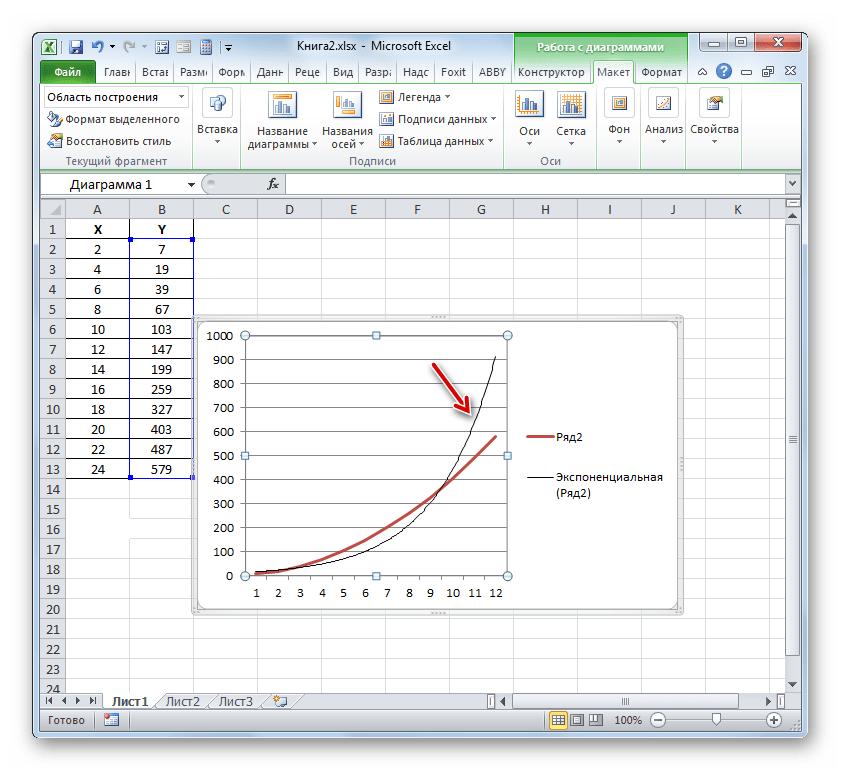
- Эксель строит прямо на плоскости построения графика линию тренда в виде дополнительной черной кривой.
- Теперь нашей задачей является отобразить собственно коэффициент детерминации. Кликаем правой кнопкой мыши по линии тренда. Активируется контекстное меню. Останавливаем выбор в нем на пункте «Формат линии тренда…».
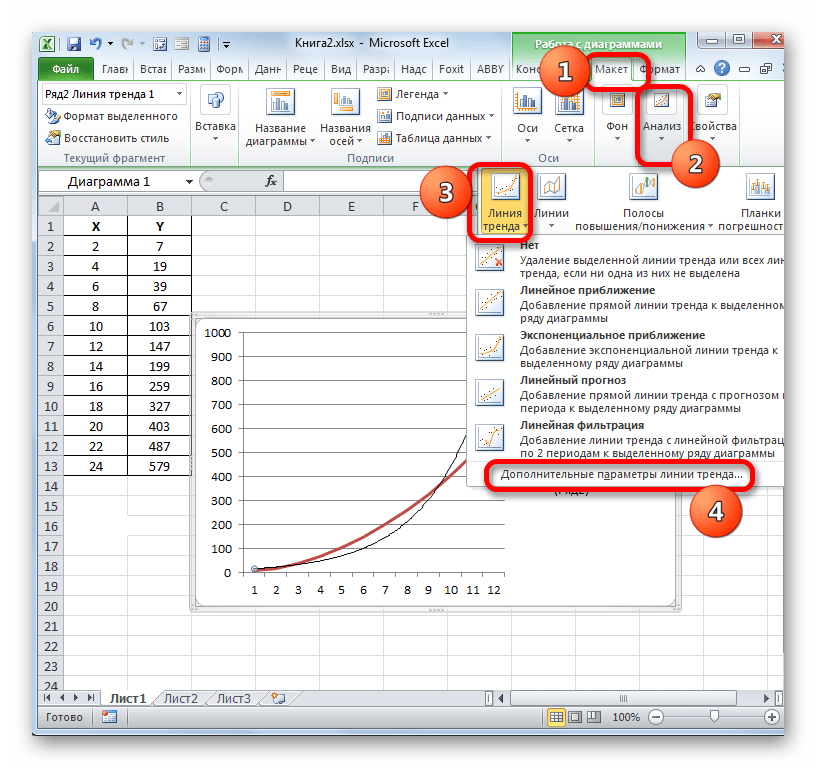
Для выполнения перехода в окно формата линии тренда можно выполнить альтернативное действие. Выделяем линию тренда кликом по ней левой кнопки мыши. Перемещаемся во вкладку «Макет». Клацаем по кнопке «Линия тренда» в блоке «Анализ». В открывшемся списке клацаем по самому последнему пункту перечня действий – «Дополнительные параметры линии тренда…».
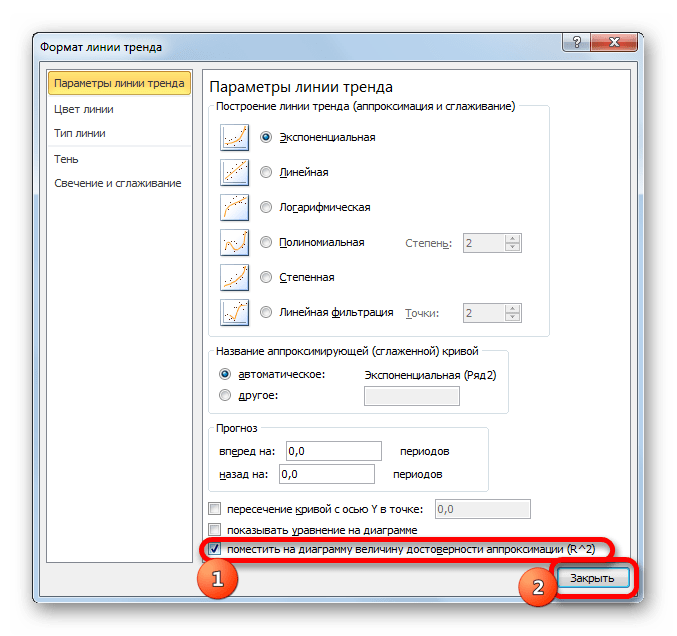
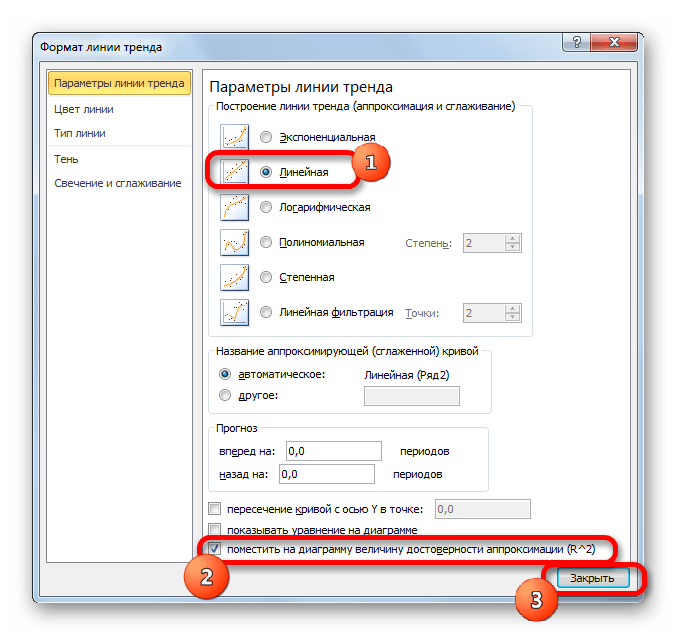
- После любого из двух вышеуказанных действий запускается окошко формата, в котором можно произвести дополнительные настройки. В частности, для выполнения нашей задачи необходимо установить флажок напротив пункта «Поместить на диаграмму величину достоверности аппроксимации (R^2)». Он размещен в самом низу окна. То есть, таким образом мы включаем отображение коэффициента детерминации на области построения. Затем не забываем нажать на кнопку «Закрыть» внизу текущего окна.
- Значение достоверности аппроксимации, то есть, величина коэффициента детерминации, будет отображено на листе в области построения. В данном случае эта величина, как видим, равна 0,9242, что характеризует аппроксимацию, как модель хорошего качества.
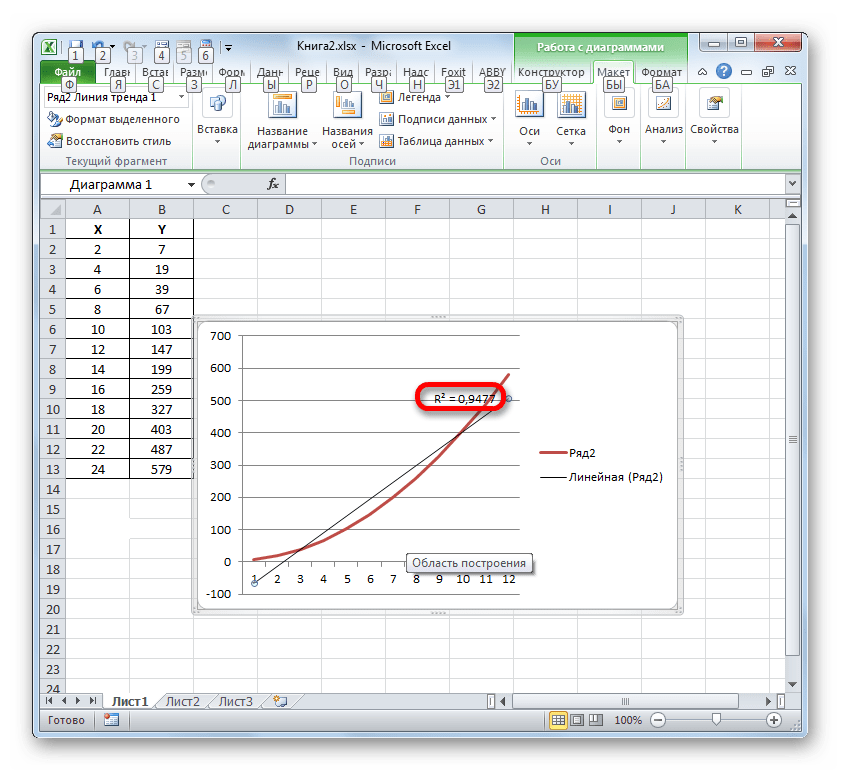
- Абсолютно точно таким образом можно устанавливать показ коэффициента детерминации для любого другого типа линии тренда. Можно менять тип линии тренда, произведя переход через кнопку на ленте или контекстное меню в окно её параметров, как было показано выше. Затем уже в самом окне в группе «Построение линии тренда» можно переключиться на другой тип. Не забываем при этом контролировать, чтобы около пункта «Поместить на диаграмму величину достоверности аппроксимации» был установлен флажок. Завершив вышеуказанные действия, щелкаем по кнопке «Закрыть» в нижнем правом углу окна.
- При линейном типе линия тренда уже имеет значение достоверности аппроксимации равное 0,9477, что характеризует эту модель, как ещё более достоверную, чем рассматриваемую нами ранее линию тренда экспоненциального типа.
- Таким образом, переключаясь между разными типами линии тренда и сравнивая их значения достоверности аппроксимации (коэффициент детерминации), можно найти тот вариант, модель которого наиболее точно описывает представленный график. Вариант с самым высоким показателем коэффициента детерминации будет наиболее достоверным. На его основе можно строить самый точный прогноз.
Например, для нашего случая опытным путем удалось установить, что самый высокий уровень достоверности имеет полиномиальный тип линии тренда второй степени. Коэффициент детерминации в данном случае равен 1. Это говорит о том, что указанная модель абсолютно достоверная, что означает полное исключение погрешностей.
Но, в то же время, это совсем не значит, что для другого графика тоже наиболее достоверным окажется именно этот тип линии тренда. Оптимальный выбор типа линии тренда зависит от типа функции, на основании которой был построен график. Если пользователь не обладает достаточным объемом знаний, чтобы «на глаз» прикинуть наиболее качественный вариант, то единственным выходом определения лучшего прогноза является как раз сравнение коэффициентов детерминации, как было показано на примере выше.
Читайте также:
Построение линии тренда в Excel
Аппроксимация в Excel
В Экселе существуют два основных варианта вычисления коэффициента детерминации: использование оператора КВПИРСОН и применение инструмента «Регрессия» из пакета инструментов «Анализ данных». При этом первый из этих вариантов предназначен для использования только в процессе обработки линейной функции, а другой вариант можно использовать практически во всех ситуациях. Кроме того, существует возможность отображения коэффициента детерминации для линии трендов графиков в качестве величины достоверности аппроксимации. С помощью данного показателя имеется возможность определить тип линии тренда, который располагает самым высоким уровнем достоверности для конкретной функции.
 Наша группа в TelegramПолезные советы и помощь
Наша группа в TelegramПолезные советы и помощь
 lumpics.ru
lumpics.ru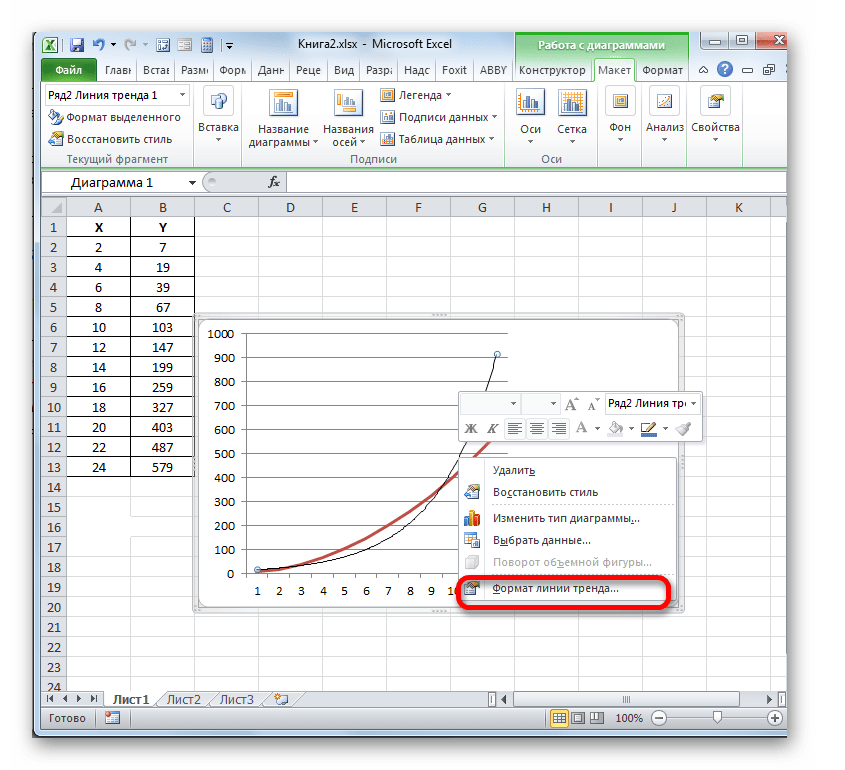




Здравствуйте.Y = 89,157Х^ — 864,6Х + 5550,6 (R^ = 0,26). что означает эти цифры, откуда они
В зависимости от уровня коэффициента детерминации, принято разделять регрессионные модели (РМ) на три группы: 0,8 — 1 — модель хорошего качества; 0,5 — 0,8 — модель приемлемого качества; 0 — 0,5 — модель плохого качества. Однако в любом случае о корректном использовании РМ для прогноза можно говорить только после проверки гипотезы о её адекватности результатам наблюдений, которая формулируется как гипотеза о равенстве дисперсии остаточной ошибки (ДОО) РМ и дисперсии ошибки воспроизводимости отклика (ДОВО).
Даже смещённая оценка ДОВО позволяет принять решение о неадекватности РМ, либо об отсутствии оснований на данном этапе расчётов для отклонения гипотезы о её адекватности. Подобный подход является решением давно существующей проблемы проверки гипотезы об адекватности РМ.
Строго говоря, по данным пассивного регрессионного эксперимента получить несмещённую оценку ДОВО невозможно. Задача оценки ДОВО долгое время являлась камнем преткновения статистической практики в регрессионном анализе. Поэтому при обработке данных всегда сохранялось сомнение в отношении адекватности полученной РМ ошибке воспроизводимости отклика. До недавнего времени требование адекватности РМ формулировалось косвенно, например, как требование получить максимальный коэффициент детерминации R2.
В книгах [1] Цейтлин Н. А. Из опыта аналитического статистика. — М.: Солар, 2007. — 906 с. и [2] Горбач А. Н., Цейтлин Н. А. Покупательское поведение: анализ спонтанных последовательностей и регрессионных моделей в маркетинговых исследованиях. — Киев: Освіта України, 2011. — 298 с. описана методика вычисления смещённой оценки ДОВО по данным пассивного регрессионного эксперимента. Эта оценка позволяет пользоваться общепринятой гипотезой об адекватности РМ.
У меня не вопрос. А благодарность разработчикам сайта. Спасибо за понятные и доступные разъяснения при построении требуемых данных.
В разобранных примерах проблем не возникает. Однако, если в линейной модели y=a +bx обнулить константу, начинаются чудеса.
Новый полученный коэффициент детерминации окажется больше первоначального. Это означает, что модель потерявшая одну степень свободы, лучше аппроксимирует исходные данные, чем первоначальная — сплошной бред.
Вывод. В опции Регрессия имеются явные недоработки.
Пример.
Исходные данные:
1,841471 1
2,909297 2
3,14112 3
3,243198 4
4,041076 5
5,720585 6
7,656987 7
8,989358 8
9,412118 9
9,455979 10
10,00001 11
11,46343 12
13,42017 13
14,99061 14
15,65029 15
получены по формуле .y=x+sinx
Берем модель y=a+bx и находим
ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R 0,986714919
R-квадрат 0,973606331
Нормированный R-квадрат 0,971576049
Стандартная ошибка 0,765569136
Наблюдения 1 5
Дисперсионный анализ
df SS MS F Значимость F
Регрессия 1 281,0579051 281,0579051 479,5423556 1,20615E-11
Остаток 13 7,619249319 0,586096101
Итого 14 288,6771544
Коэффициенты Стандартная ошибка t-статистика P-Значение
Y-пересечение 0,113947 0,415978241 0,273925746 0,788445813
Переменная X 1,001887 0,045751507 21,89845555 1,20615E-11
P-Значение показывает, что константу надо обнулить a=0 . Снова обращаемся к Регрессии
ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R 0,997002
R-квадрат 0,994013
Нормированный R-квадрат 0,922584
Стандартная ошибка 0,739847
Наблюдения 15
Дисперсионный анализ
df SS MS F Значимость F
Регрессия 1 1272,235 1272,235 2324,254 4,8053E-16
Остаток 14 7,663227 0,547373
Итого 15 1279,898 ? и здесь напахали TSS=288,6771544 и не должно меняться от вида модели.
То, что называется «приплыли»:
R*-квадрат 0,994013 > 0,9736; F*=2324,254 > 479,542.
Однако, основной показатель RSS=7,619 < SSR*=7,663 говорит, что первоначальная модель, все-таки точнее (в смысле МНК).
Могу предположить, что разработчики Регрессии не учли, что при насильственном изменении модели, Теорема о 3-х дисперсиях не выполняется: TSS 288,6771544 > )