Вычисление доверительного интервала в Microsoft Excel

Одним из методов решения статистических задач является вычисление доверительного интервала. Он используется, как более предпочтительная альтернатива точечной оценке при небольшом объеме выборки. Нужно отметить, что сам процесс вычисления доверительного интервала довольно сложный. Но инструменты программы Эксель позволяют несколько упростить его. Давайте узнаем, как это выполняется на практике.

Читайте также: Статистические функции в Экселе

Процедура вычисления

Этот метод используется при интервальной оценке различных статистических величин. Главная задача данного расчета – избавится от неопределенностей точечной оценки.

В Экселе существуют два основных варианта произвести вычисления с помощью данного метода: когда дисперсия известна, и когда она неизвестна. В первом случае для вычислений применяется функция ДОВЕРИТ.НОРМ, а во втором — ДОВЕРИТ.СТЮДЕНТ.

Способ 1: функция ДОВЕРИТ.НОРМ

Оператор ДОВЕРИТ.НОРМ, относящийся к статистической группе функций, впервые появился в Excel 2010. В более ранних версиях этой программы используется его аналог ДОВЕРИТ. Задачей этого оператора является расчет доверительного интервала с нормальным распределением для средней генеральной совокупности.

Его синтаксис выглядит следующим образом:

=ДОВЕРИТ.НОРМ(альфа;стандартное_откл;размер)

«Альфа» — аргумент, указывающий на уровень значимости, который применяется для расчета доверительного уровня. Доверительный уровень равняется следующему выражению:

(1-«Альфа»)*100

«Стандартное отклонение» — это аргумент, суть которого понятна из наименования. Это стандартное отклонение предлагаемой выборки.

«Размер» — аргумент, определяющий величину выборки.

Все аргументы данного оператора являются обязательными.

Функция ДОВЕРИТ имеет точно такие же аргументы и возможности, что и предыдущая. Её синтаксис таков:

=ДОВЕРИТ(альфа;стандартное_откл;размер)

Как видим, различия только в наименовании оператора. Указанная функция в целях совместимости оставлена в Excel 2010 и в более новых версиях в специальной категории «Совместимость». В версиях же Excel 2007 и ранее она присутствует в основной группе статистических операторов.

Граница доверительного интервала определяется при помощи формулы следующего вида:

X+(-)ДОВЕРИТ.НОРМ

Где X – это среднее выборочное значение, которое расположено посередине выбранного диапазона.

Теперь давайте рассмотрим, как рассчитать доверительный интервал на конкретном примере. Было проведено 12 испытаний, вследствие которых были получены различные результаты, занесенные в таблицу. Это и есть наша совокупность. Стандартное отклонение равно 8. Нам нужно рассчитать доверительный интервал при уровне доверия 97%.

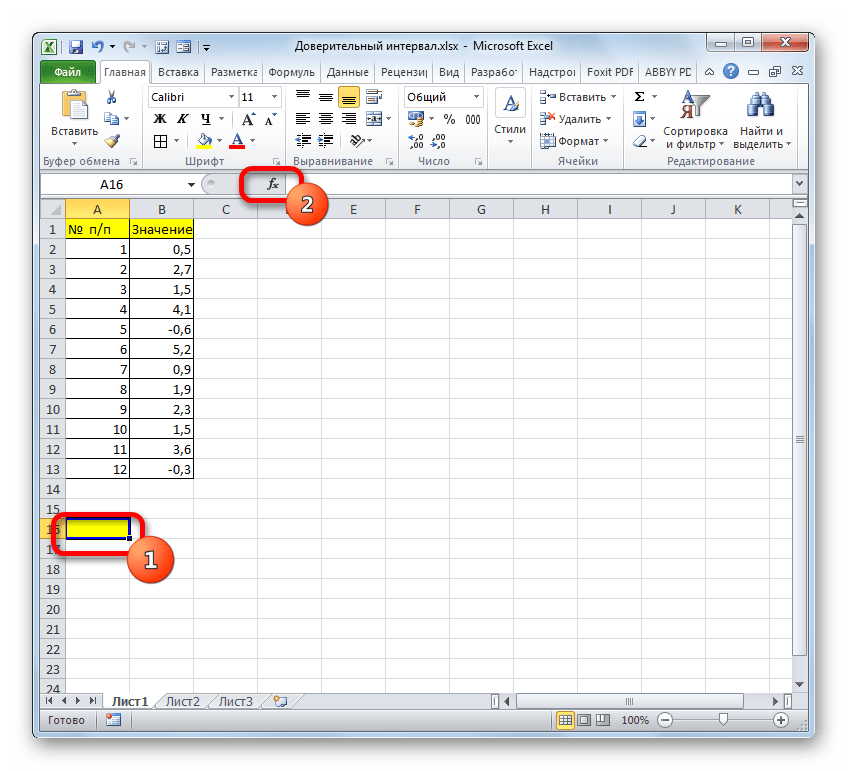
1. Выделяем ячейку, куда будет выводиться результат обработки данных. Щелкаем по кнопке «Вставить функцию».

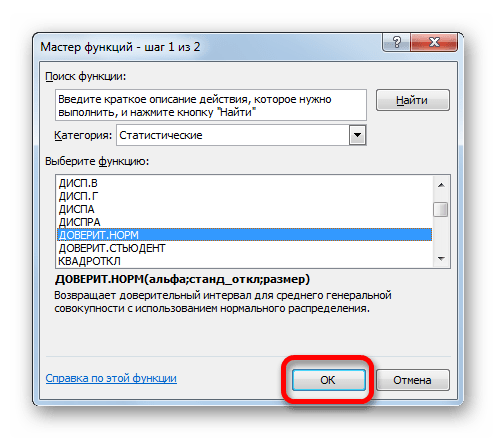
2. Появляется Мастер функций. Переходим в категорию «Статистические» и выделяем наименование «ДОВЕРИТ.НОРМ». После этого клацаем по кнопке «OK».

3. Открывается окошко аргументов. Его поля закономерно соответствуют наименованиям аргументов.
   Устанавливаем курсор в первое поле – «Альфа». Тут нам следует указать уровень значимости. Как мы помним, уровень доверия у нас равен 97%. В то же время мы говорили, что он рассчитывается таким путем:

   (1-«Альфа»)*100

   Значит, чтобы посчитать уровень значимости, то есть, определить значение «Альфа» следует применить формулу такого вида:

   (1-уровень доверия)/100

   То есть, подставив значение, получаем:

   (1-97)/100

   Путем нехитрых расчетов узнаем, что аргумент «Альфа» равен 0,03. Вводим данное значение в поле.

   Как известно, по условию стандартное отклонение равно 8. Поэтому в поле «Стандартное отклонение» просто записываем это число.

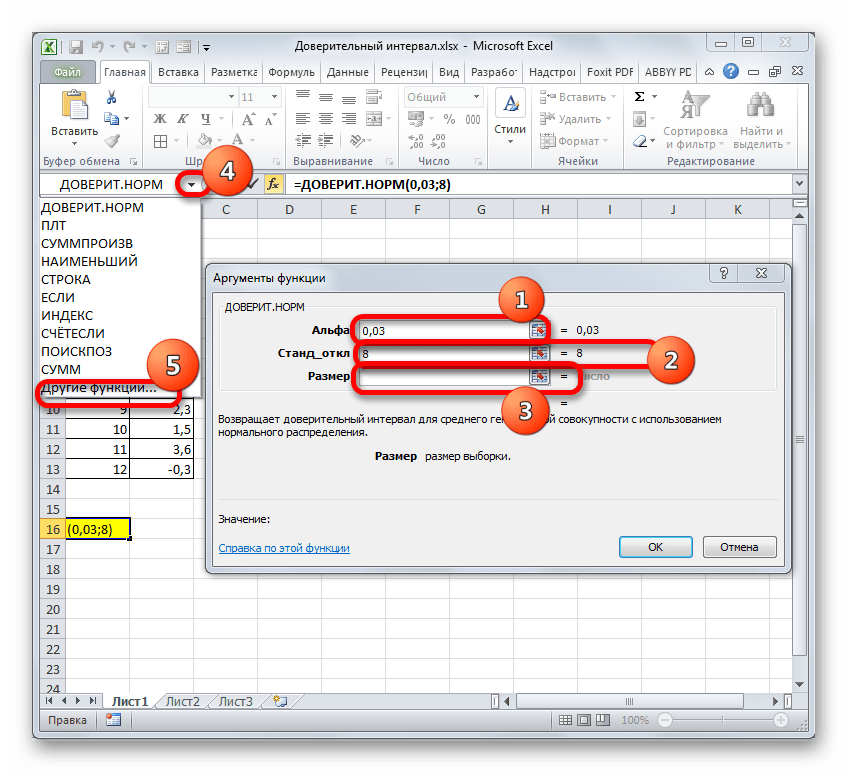
   В поле «Размер» нужно ввести количество элементов проведенных испытаний. Как мы помним, их 12. Но чтобы автоматизировать формулу и не редактировать её каждый раз при проведении нового испытания, давайте зададим данное значение не обычным числом, а при помощи оператора СЧЁТ. Итак, устанавливаем курсор в поле «Размер», а затем кликаем по треугольнику, который размещен слева от строки формул.

   Появляется список недавно применяемых функций. Если оператор СЧЁТ применялся вами недавно, то он должен быть в этом списке. В таком случае, нужно просто кликнуть по его наименованию. В обратном же случае, если вы его не обнаружите, то переходите по пункту «Другие функции…».


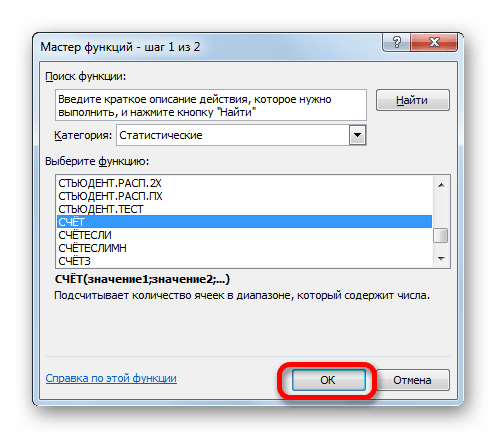
4. Появляется уже знакомый нам Мастер функций. Опять перемещаемся в группу «Статистические». Выделяем там наименование «СЧЁТ». Клацаем по кнопке «OK».

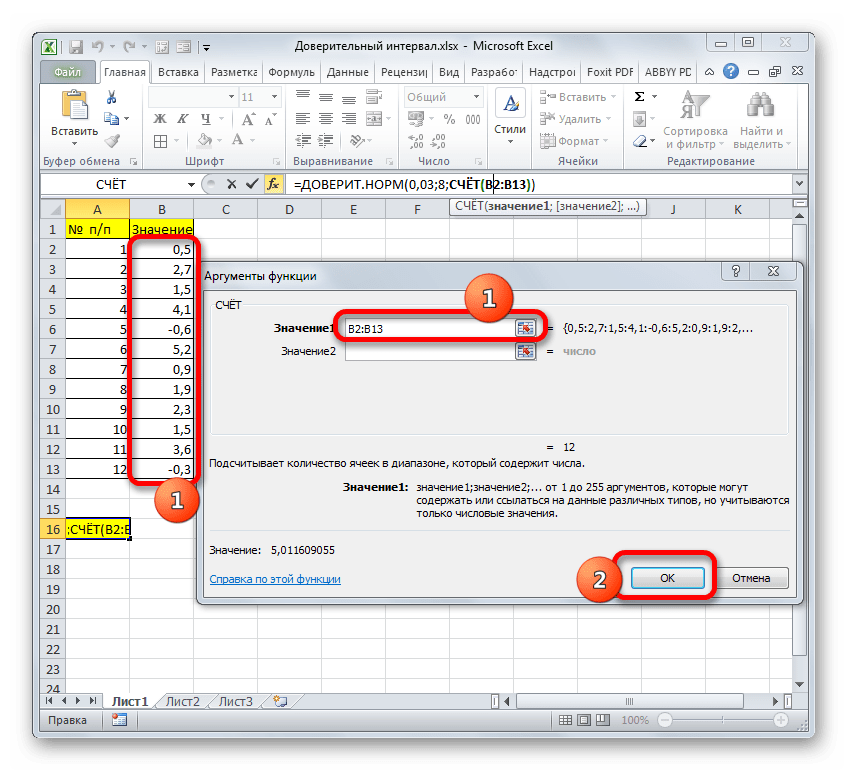
5. Появляется окно аргументов вышеуказанного оператора. Данная функция предназначена для того, чтобы вычислять количество ячеек в указанном диапазоне, которые содержат числовые значения. Синтаксис её следующий:

   =СЧЁТ(значение1;значение2;…)

   Группа аргументов «Значения» представляет собой ссылку на диапазон, в котором нужно рассчитать количество заполненных числовыми данными ячеек. Всего может насчитываться до 255 подобных аргументов, но в нашем случае понадобится лишь один.

   Устанавливаем курсор в поле «Значение1» и, зажав левую кнопку мыши, выделяем на листе диапазон, который содержит нашу совокупность. Затем его адрес будет отображен в поле. Клацаем по кнопке «OK».


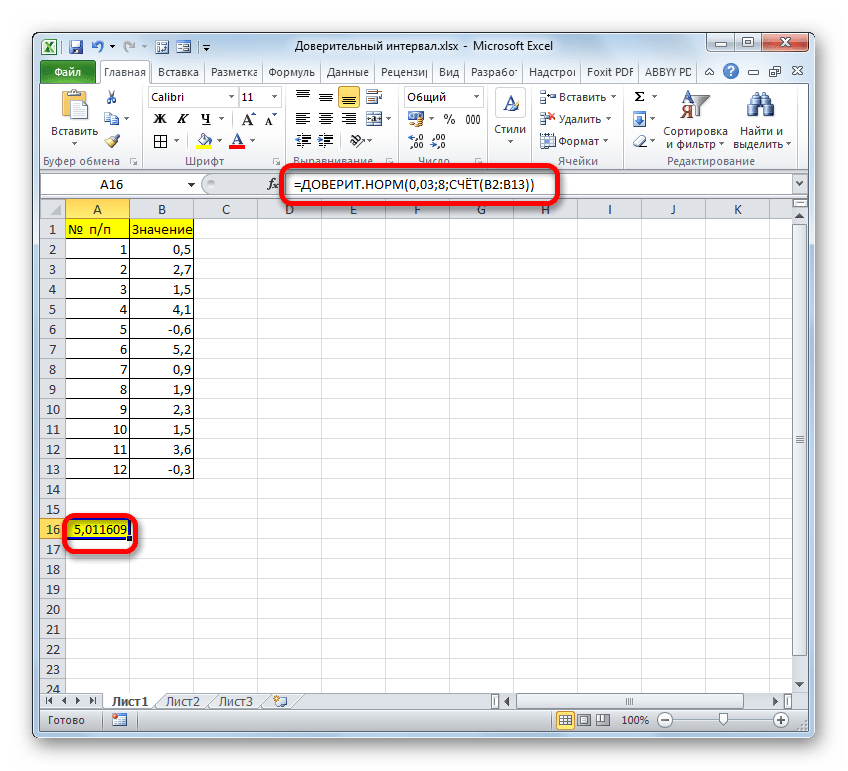
6. После этого приложение произведет вычисление и выведет результат в ту ячейку, где она находится сама. В нашем конкретном случае формула получилась такого вида:

   =ДОВЕРИТ.НОРМ(0,03;8;СЧЁТ(B2:B13))

   Общий результат вычислений составил 5,011609.


7. Но это ещё не все. Как мы помним, граница доверительного интервала вычисляется путем сложения и вычитания от среднего выборочного значения результата вычисления ДОВЕРИТ.НОРМ. Таким способом рассчитывается соответственно правая и левая граница доверительного интервала. Само среднее выборочное значение можно рассчитать при помощи оператора СРЗНАЧ.

   Данный оператор предназначен для расчета среднего арифметического значения выбранного диапазона чисел. Он имеет следующий довольно простой синтаксис:

   =СРЗНАЧ(число1;число2;…)

   Аргумент «Число» может быть как отдельным числовым значением, так и ссылкой на ячейки или даже целые диапазоны, которые их содержат.

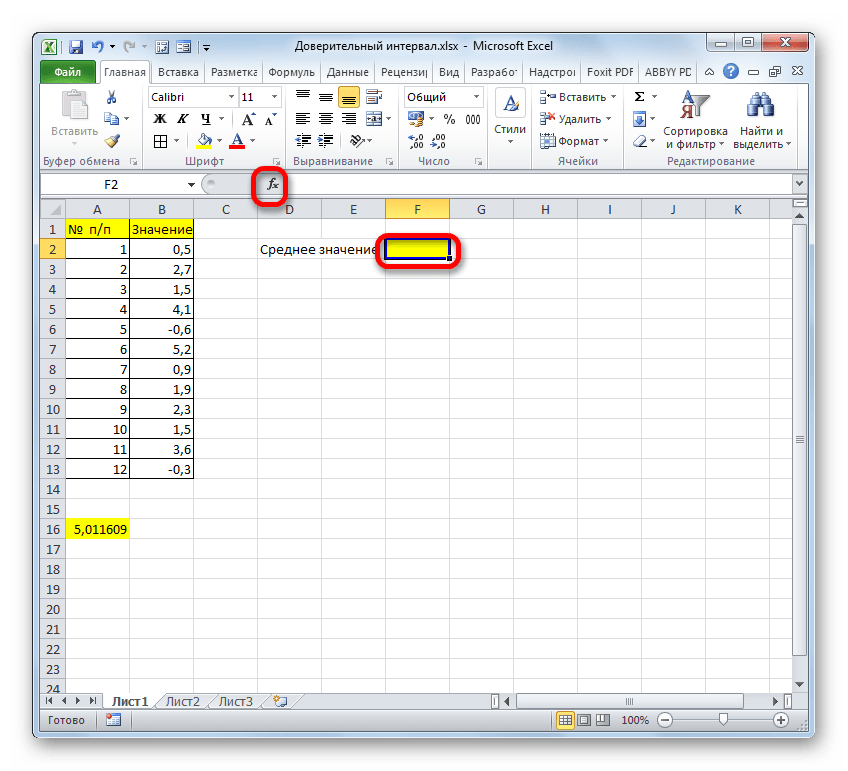
   Итак, выделяем ячейку, в которую будет выводиться расчет среднего значения, и щелкаем по кнопке «Вставить функцию».


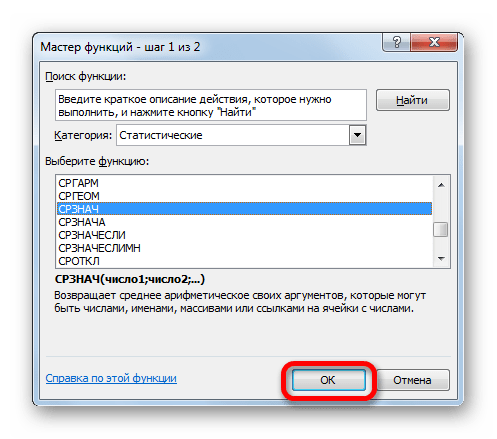
8. Открывается Мастер функций. Снова переходим в категорию «Статистические» и выбираем из списка наименование «СРЗНАЧ». Как всегда, клацаем по кнопке «OK».

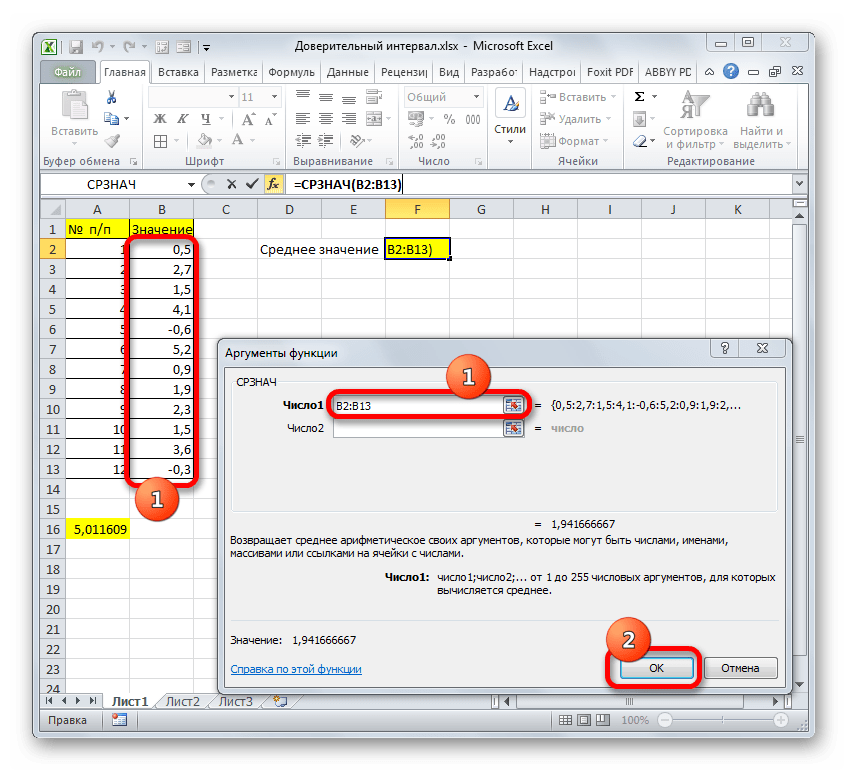
9. Запускается окно аргументов. Устанавливаем курсор в поле «Число1» и с зажатой левой кнопкой мыши выделяем весь диапазон значений. После того, как координаты отобразились в поле, клацаем по кнопке «OK».

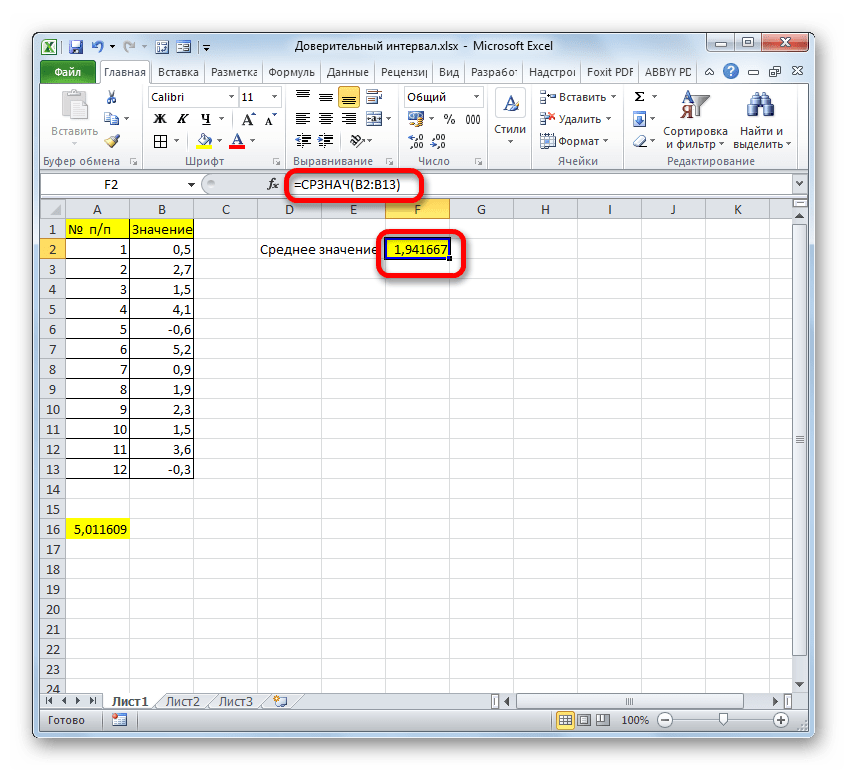
10. После этого СРЗНАЧ выводит результат расчета в элемент листа.

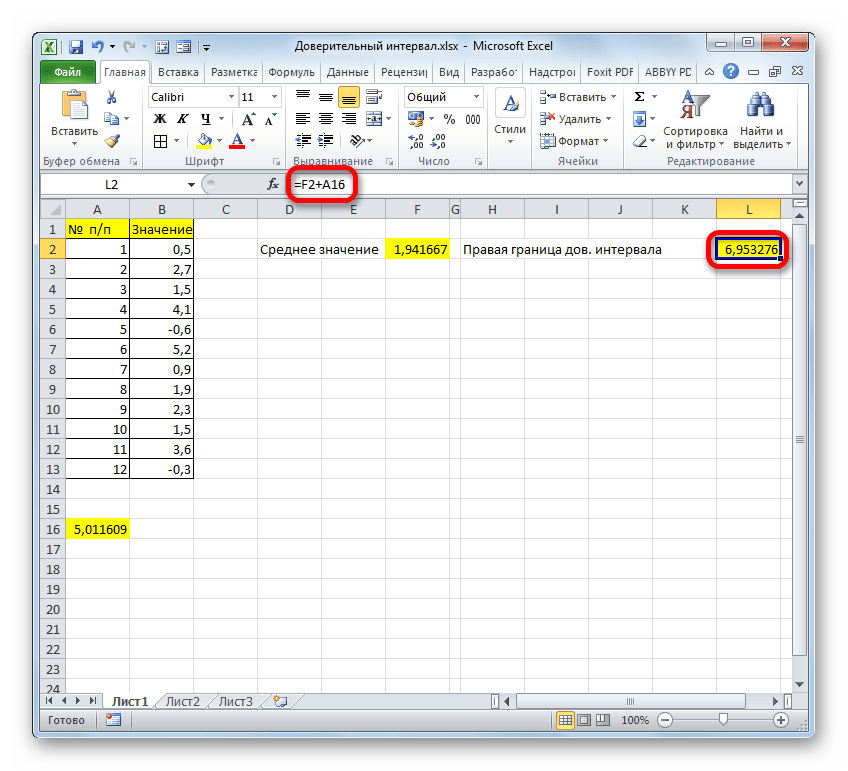
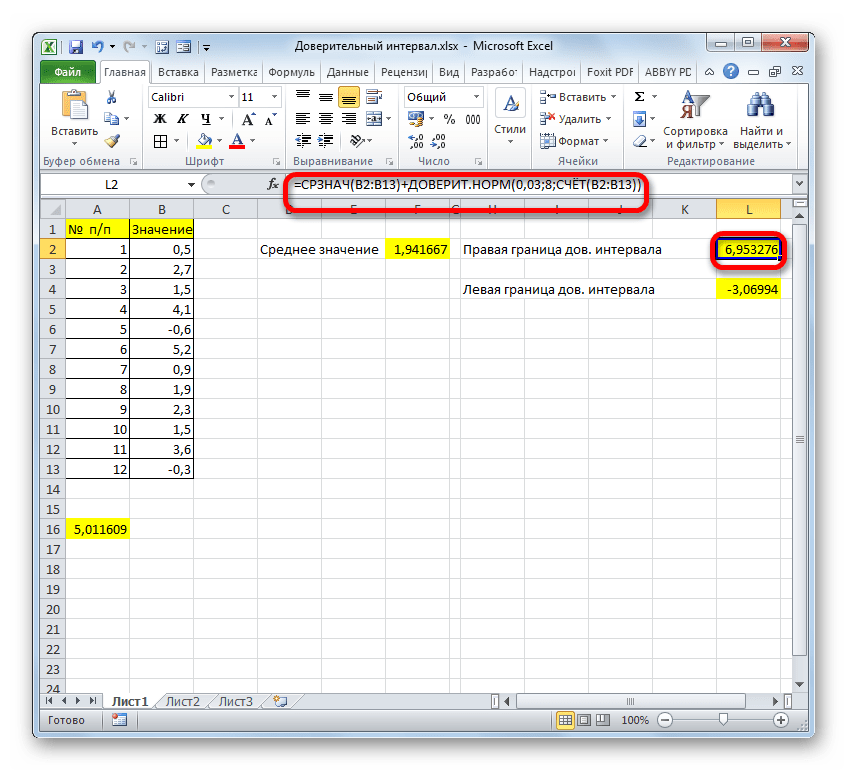
11. Производим расчет правой границы доверительного интервала. Для этого выделяем отдельную ячейку, ставим знак «=» и складываем содержимое элементов листа, в которых расположены результаты вычислений функций СРЗНАЧ и ДОВЕРИТ.НОРМ. Для того, чтобы выполнить расчет, жмем на клавишу Enter. В нашем случае получилась следующая формула:

    =F2+A16

    Результат вычисления: 6,953276


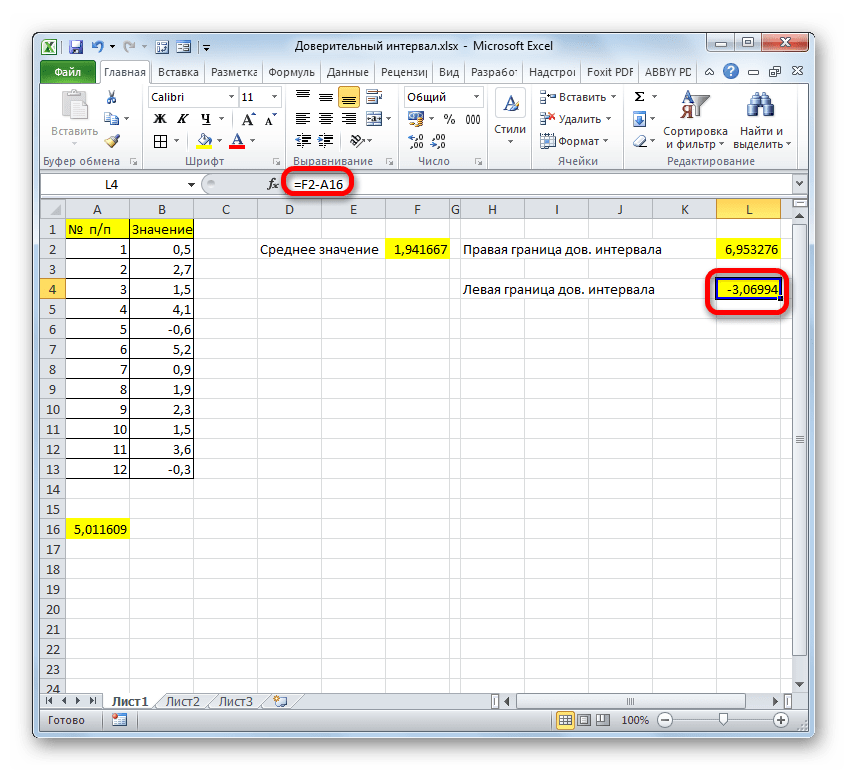
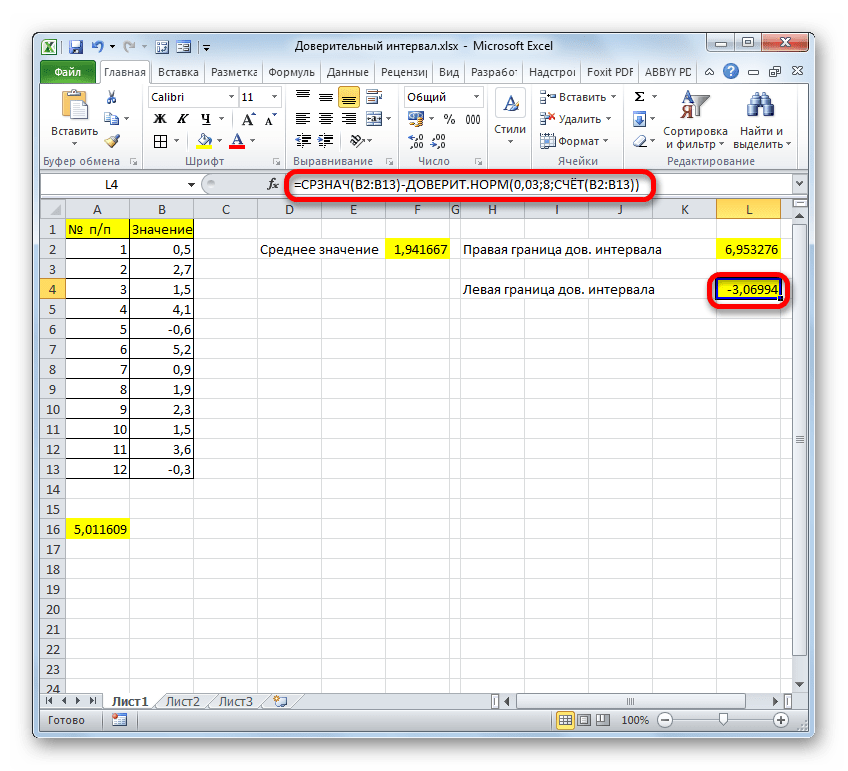
12. Таким же образом производим вычисление левой границы доверительного интервала, только на этот раз от результата вычисления СРЗНАЧ отнимаем результат вычисления оператора ДОВЕРИТ.НОРМ. Получается формула для нашего примера следующего типа:

    =F2-A16

    Результат вычисления: -3,06994


13. Мы попытались подробно описать все действия по вычислению доверительного интервала, поэтому детально расписали каждую формулу. Но можно все действия соединить в одной формуле. Вычисление правой границы доверительного интервала можно записать так:

    =СРЗНАЧ(B2:B13)+ДОВЕРИТ.НОРМ(0,03;8;СЧЁТ(B2:B13))


14. Аналогичное вычисление левой границы будет выглядеть так:

    =СРЗНАЧ(B2:B13)-ДОВЕРИТ.НОРМ(0,03;8;СЧЁТ(B2:B13))

Способ 2: функция ДОВЕРИТ.СТЮДЕНТ

Кроме того, в Экселе есть ещё одна функция, которая связана с вычислением доверительного интервала – ДОВЕРИТ.СТЮДЕНТ. Она появилась, только начиная с Excel 2010. Данный оператор выполняет вычисление доверительного интервала генеральной совокупности с использованием распределения Стьюдента. Его очень удобно использовать в том случае, когда дисперсия и, соответственно, стандартное отклонение неизвестны. Синтаксис оператора такой:

=ДОВЕРИТ.СТЬЮДЕНТ(альфа;стандартное_откл;размер)

Как видим, наименования операторов и в этом случае остались неизменными.

Посмотрим, как рассчитать границы доверительного интервала с неизвестным стандартным отклонением на примере всё той же совокупности, что мы рассматривали в предыдущем способе. Уровень доверия, как и в прошлый раз, возьмем 97%.

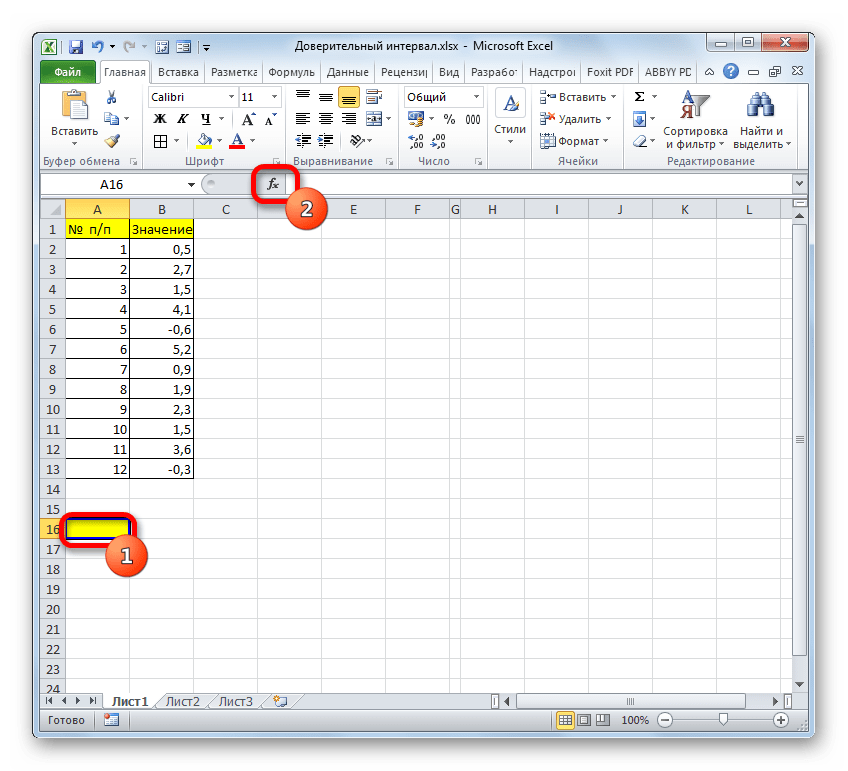
1. Выделяем ячейку, в которую будет производиться расчет. Клацаем по кнопке «Вставить функцию».

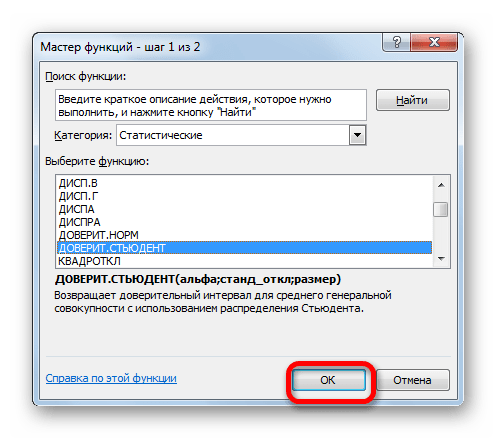
2. В открывшемся Мастере функций переходим в категорию «Статистические». Выбираем наименование «ДОВЕРИТ.СТЮДЕНТ». Клацаем по кнопке «OK».

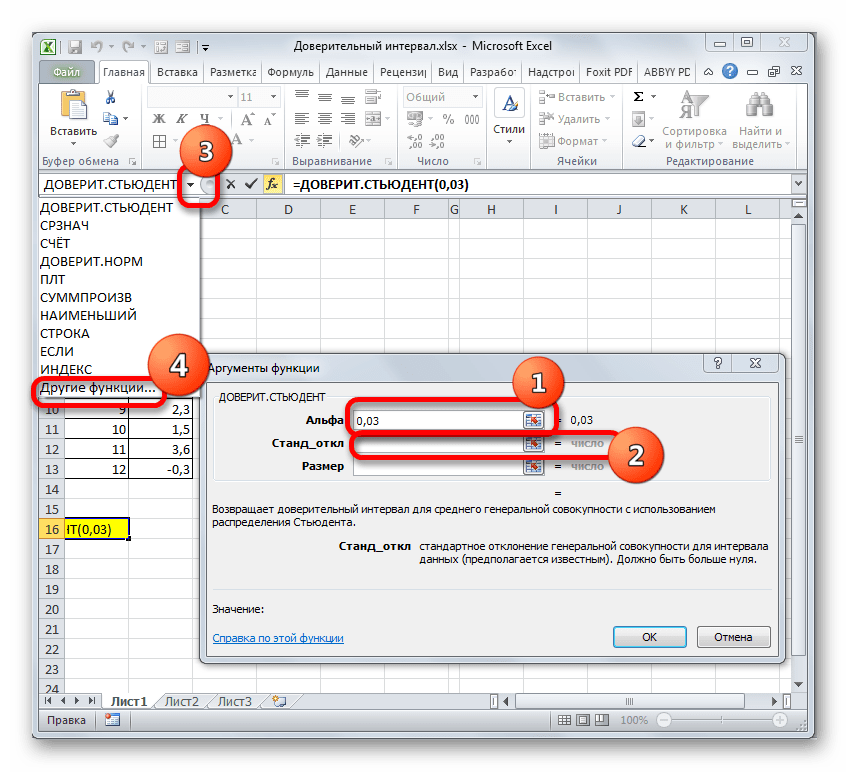
3. Производится запуск окна аргументов указанного оператора.

   В поле «Альфа», учитывая, что уровень доверия составляет 97%, записываем число 0,03. Второй раз на принципах расчета данного параметра останавливаться не будем.

   После этого устанавливаем курсор в поле «Стандартное отклонение». На этот раз данный показатель нам неизвестен и его требуется рассчитать. Делается это при помощи специальной функции – СТАНДОТКЛОН.В. Чтобы вызвать окно данного оператора, кликаем по треугольнику слева от строки формул. Если в открывшемся списке не находим нужного наименования, то переходим по пункту «Другие функции…».


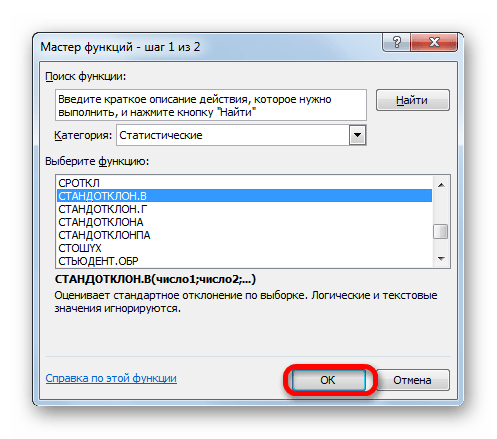
4. Запускается Мастер функций. Перемещаемся в категорию «Статистические» и отмечаем в ней наименование «СТАНДОТКЛОН.В». Затем клацаем по кнопке «OK».

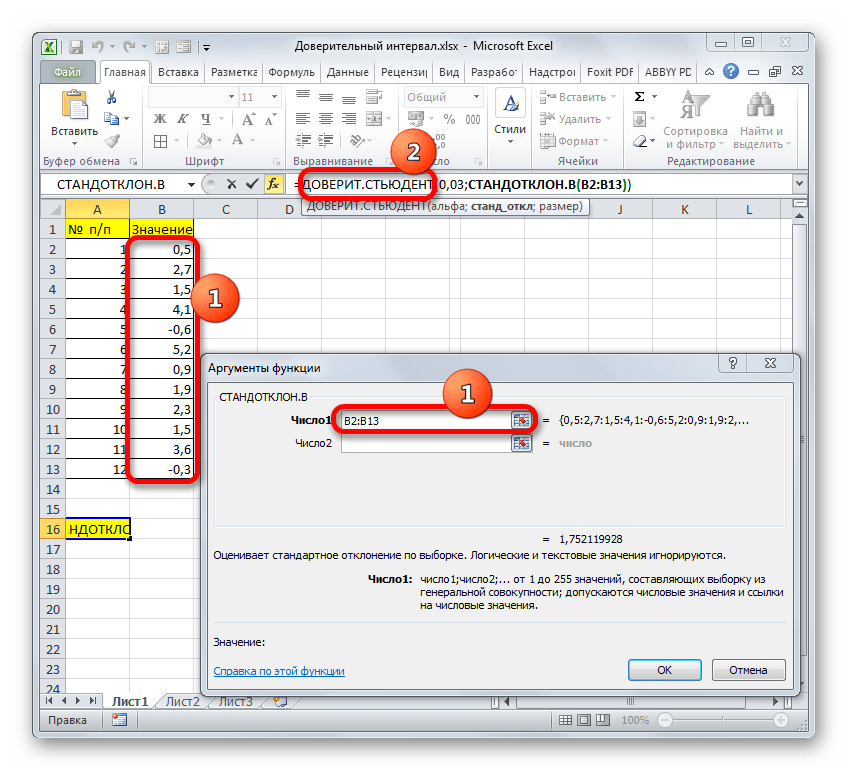
5. Открывается окно аргументов. Задачей оператора СТАНДОТКЛОН.В является определение стандартного отклонения при выборке. Его синтаксис выглядит так:

   =СТАНДОТКЛОН.В(число1;число2;…)

   Нетрудно догадаться, что аргумент «Число» — это адрес элемента выборки. Если выборка размещена единым массивом, то можно, использовав только один аргумент, дать ссылку на данный диапазон.

   Устанавливаем курсор в поле «Число1» и, как всегда, зажав левую кнопку мыши, выделяем совокупность. После того, как координаты попали в поле, не спешим жать на кнопку «OK», так как результат получится некорректным. Прежде нам нужно вернуться к окну аргументов оператора ДОВЕРИТ.СТЮДЕНТ, чтобы внести последний аргумент. Для этого кликаем по соответствующему наименованию в строке формул.


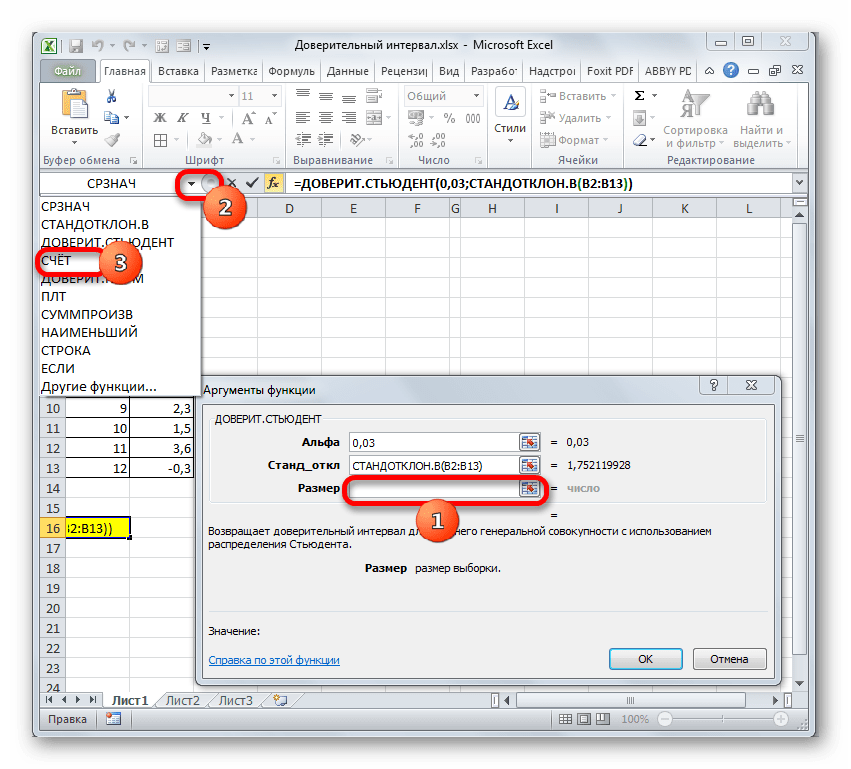
6. Снова открывается окно аргументов уже знакомой функции. Устанавливаем курсор в поле «Размер». Опять жмем на уже знакомый нам треугольник для перехода к выбору операторов. Как вы поняли, нам нужно наименование «СЧЁТ». Так как мы использовали данную функцию при вычислениях в предыдущем способе, в данном списке она присутствует, так что просто щелкаем по ней. Если же вы её не обнаружите, то действуйте по алгоритму, описанному в первом способе.

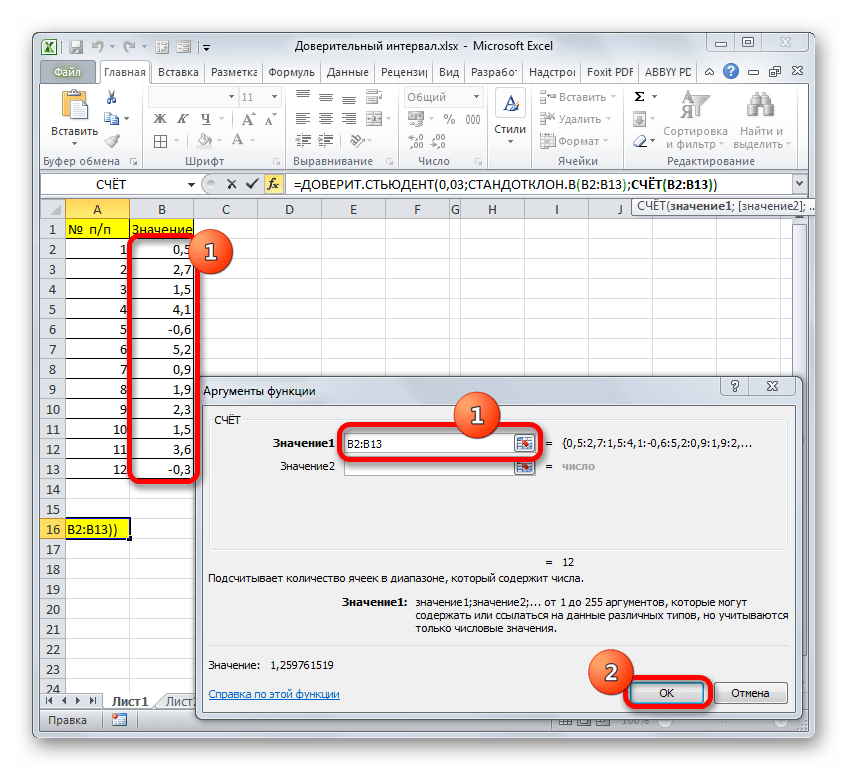
7. Попав в окно аргументов СЧЁТ, ставим курсор в поле «Число1» и с зажатой кнопкой мыши выделяем совокупность. Затем клацаем по кнопке «OK».

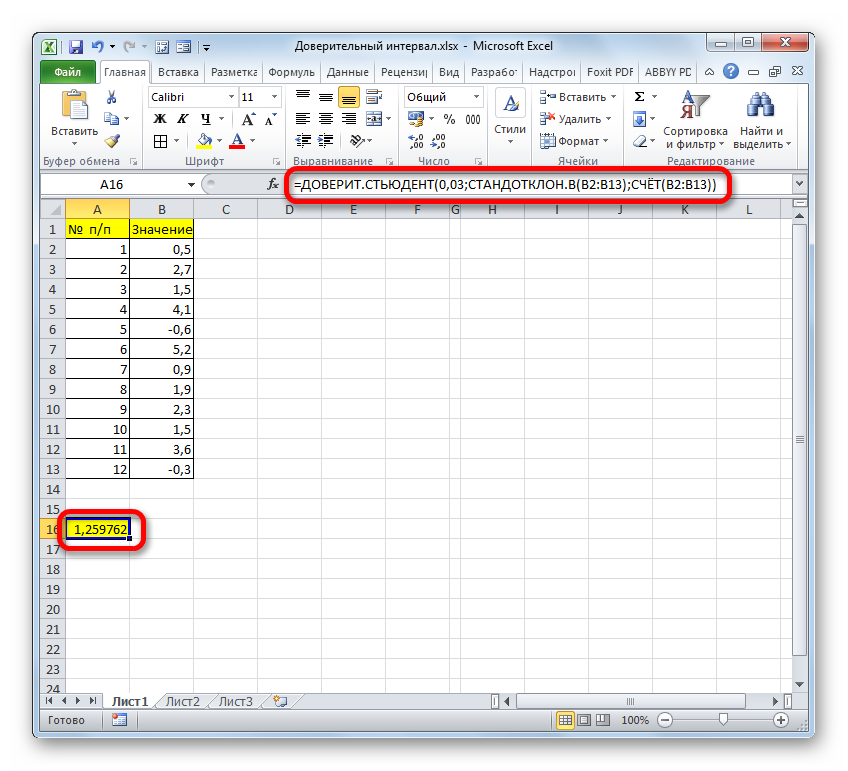
8. После этого программа производит расчет и выводит значение доверительного интервала.

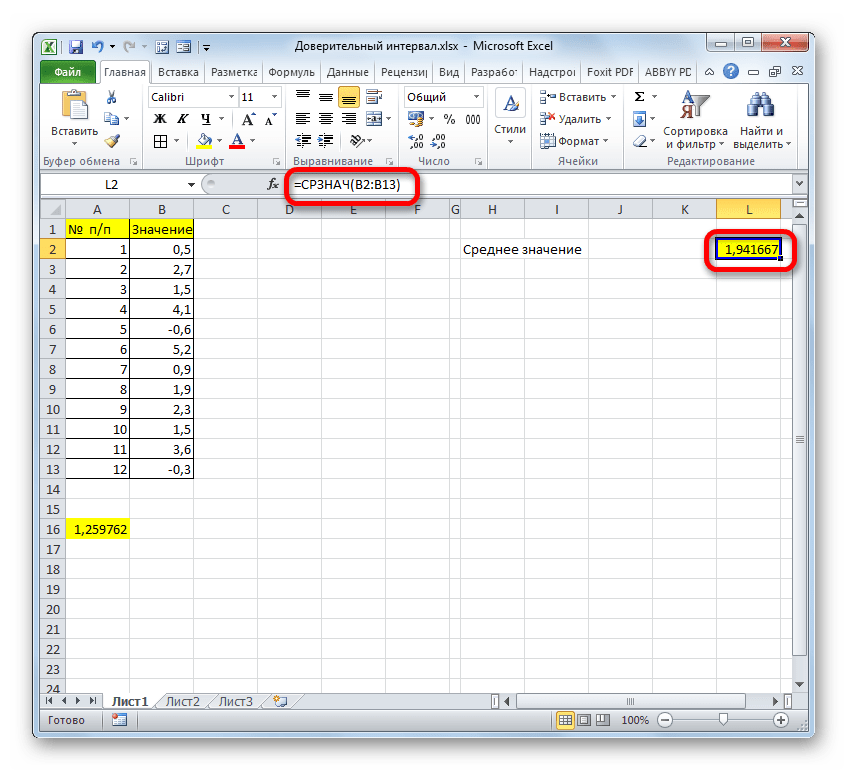
9. Для определения границ нам опять нужно будет рассчитать среднее значение выборки. Но, учитывая то, что алгоритм расчета при помощи формулы СРЗНАЧ тот же, что и в предыдущем способе, и даже результат не изменился, не будем на этом подробно останавливаться второй раз.

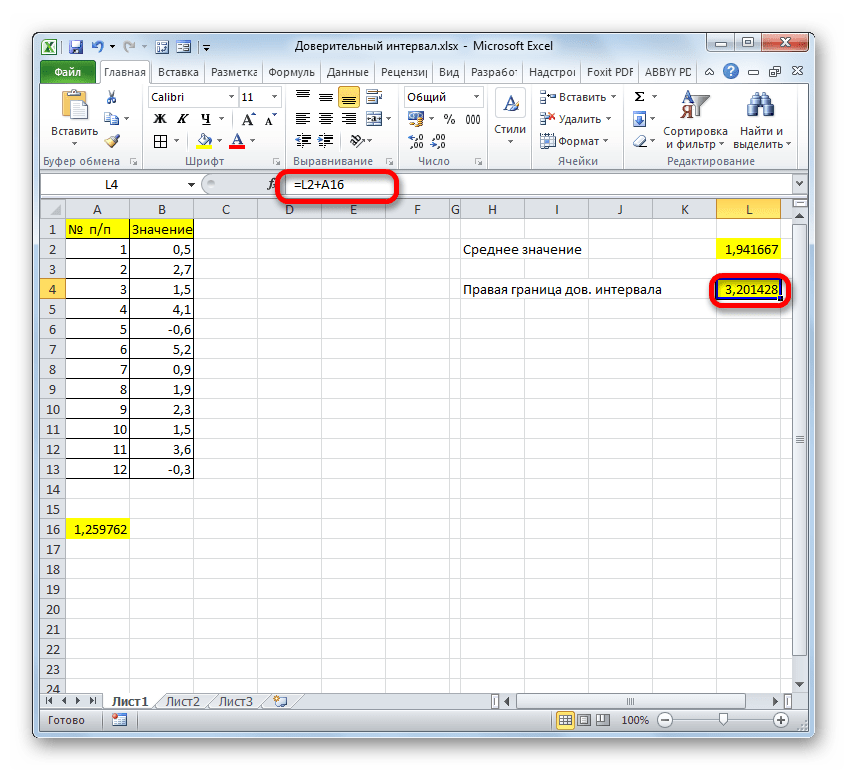
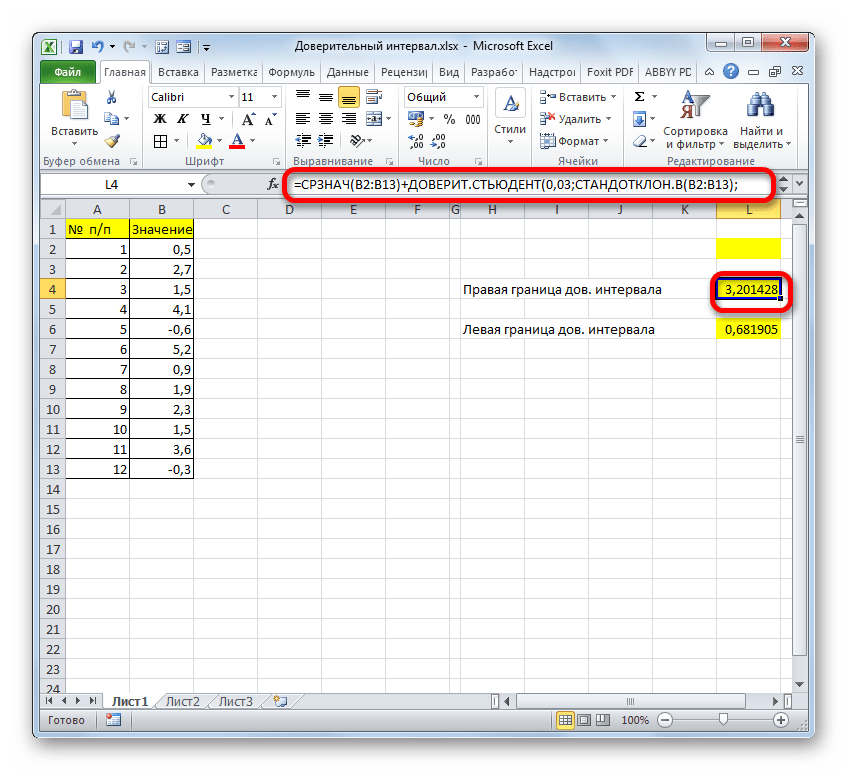
10. Сложив результаты вычисления СРЗНАЧ и ДОВЕРИТ.СТЮДЕНТ, получаем правую границу доверительного интервала.

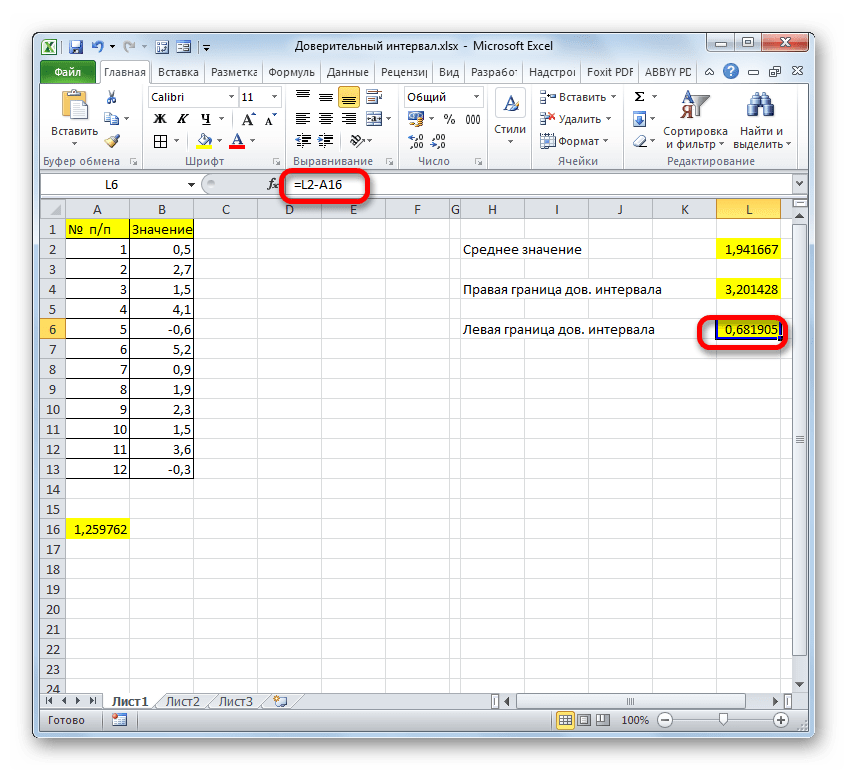
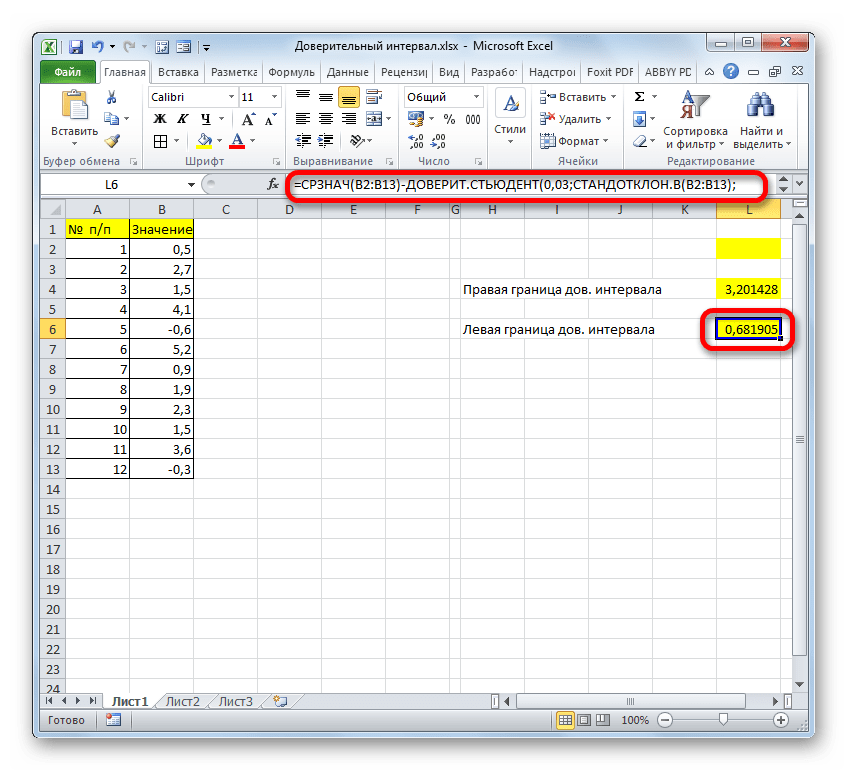
11. Отняв от результатов расчета оператора СРЗНАЧ результат расчета ДОВЕРИТ.СТЮДЕНТ, имеем левую границу доверительного интервала.

12. Если расчет записать одной формулой, то вычисление правой границы в нашем случае будет выглядеть так:

    =СРЗНАЧ(B2:B13)+ДОВЕРИТ.СТЬЮДЕНТ(0,03;СТАНДОТКЛОН.В(B2:B13);СЧЁТ(B2:B13))


13. Соответственно, формула расчета левой границы будет выглядеть так:

    =СРЗНАЧ(B2:B13)-ДОВЕРИТ.СТЬЮДЕНТ(0,03;СТАНДОТКЛОН.В(B2:B13);СЧЁТ(B2:B13))

Как видим, инструменты программы Excel позволяют существенно облегчить вычисление доверительного интервала и его границ. Для этих целей используются отдельные операторы для выборок, у которых дисперсия известна и неизвестна.

Наш Telegram каналТолько полезная информация